Difference between revisions of "WNDW: Difraksi"
Onnowpurbo (talk | contribs) (New page: Difraksi akan tampak seperti pembelokan dari gelombang pada saat menabrak sebuah objek. Hal ini merupakan efek dari “gelombang akan mengitari pojokan”. [[Image:Figure2.6.jpg|right|20...) |
Onnowpurbo (talk | contribs) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Difraksi akan tampak seperti pembelokan dari gelombang pada saat menabrak sebuah objek. Hal ini merupakan efek dari “gelombang akan mengitari pojokan”. | + | [[Difraksi]] akan tampak seperti pembelokan dari gelombang pada saat menabrak sebuah objek. Hal ini merupakan efek dari “gelombang akan mengitari pojokan”. |
| − | [[Image:Figure2.6.jpg|right|200px|thumb|Gambar 2.6: Difraksi melalui celah sempit.]] | + | [[Image:Figure2.6.jpg|right|200px|thumb|Gambar 2.6: [[Difraksi]] melalui celah sempit.]] |
| − | Bayangkan sebuah gelombang di air merambat dalam barisan gelombang yang lurus, seperti barisan gelombang yang sering kita lihat di pantai. Bayangkan jika kita meletakan penghalang benda padat, misalnya pagar kayu yang rapat, yang menghalangi pergerakan gelobang. Jika kita memotong pagar tersebut, dan membuat bukaan sempit di pagar, seperti sebuah pintu yang kecil. Dari bukaan tersebut, sebuah gelombang sirkular akan di mulai, dan akan merambat ke berbagai tempat yang tidak garis lurus dari pembukaan yang kita buat, tapi juga ke lokasi-lokasi yang ada di samping pembukaan. Jika kita melihat barisan gelombang – yang mungkin saja berupa gelombang elektromagnetik – sebagai sinar yang lurus, akan susah untuk menerangkan bagaimana caranya mencapai titik-titik yang tersembunyi di balik penghalang. Dengan model barisan gelombang, maka fenomena ini menjadi masuk akal. | + | Bayangkan sebuah gelombang di air merambat dalam barisan gelombang yang lurus, seperti barisan gelombang yang sering kita lihat di pantai. Bayangkan jika kita meletakan penghalang benda padat, misalnya pagar kayu yang rapat, yang menghalangi pergerakan gelobang. Jika kita memotong pagar tersebut, dan membuat bukaan sempit di pagar, seperti sebuah pintu yang kecil. Dari bukaan tersebut, sebuah gelombang sirkular akan di mulai, dan akan merambat ke berbagai tempat yang tidak garis lurus dari pembukaan yang kita buat, tapi juga ke lokasi-lokasi yang ada di samping pembukaan. Jika kita melihat barisan gelombang – yang mungkin saja berupa [[gelombang elektromagnetik]] – sebagai sinar yang lurus, akan susah untuk menerangkan bagaimana caranya mencapai titik-titik yang tersembunyi di balik penghalang. Dengan model barisan gelombang, maka fenomena ini menjadi masuk akal. |
[[Image:Figure2.7.jpg|left|200px|thumb|Gambar 2.7: Prinsip Huygens]] | [[Image:Figure2.7.jpg|left|200px|thumb|Gambar 2.7: Prinsip Huygens]] | ||
Prinsip Huygens memberikan sebuah model untuk mengerti perilaku ini. Bayangkan pada saat tertentu, semua titik di barisan gelombang menjadi titik awal dari gelombang kecil yang menyebar. Ide ini kemudian di kembangkan oleh Fresnel, apakah hal ini cukup untuk menjelaskan fenomena yang terjadi memang masih menjadi perdebatan. Akan tetapi untuk kebutuhan kita, model Huygens dapat menjelaskan effek yang terjadi dengan cukup baik. | Prinsip Huygens memberikan sebuah model untuk mengerti perilaku ini. Bayangkan pada saat tertentu, semua titik di barisan gelombang menjadi titik awal dari gelombang kecil yang menyebar. Ide ini kemudian di kembangkan oleh Fresnel, apakah hal ini cukup untuk menjelaskan fenomena yang terjadi memang masih menjadi perdebatan. Akan tetapi untuk kebutuhan kita, model Huygens dapat menjelaskan effek yang terjadi dengan cukup baik. | ||
| − | [[Image:Figure2.8.jpg|right|200px|thumb|Gambar 2.8: Difraksi Melalui Puncak Gunung.]] | + | [[Image:Figure2.8.jpg|right|200px|thumb|Gambar 2.8: [[Difraksi]] Melalui Puncak Gunung.]] |
| − | Melalui kemampuan untuk | + | Melalui kemampuan untuk [[difraksi]], gelombang akan “membelok” melewati pojokan atau melalui pembukaan kecil yang ada di penghalang. Untuk panjang gelombang cahaya biasanya terlalu kecil untuk manusia untuk melihat efek ini secara langsung. Pada [[gelombang mikro]], dimana panjang gelombangnya beberapa centimeter, akan menampakan efek difraksi saat gelombang menabrak tembok, puncak gunung, dan berbagai halangan lainnya. Tampaknya seperti penghalang akan menyebabkan gelombang mengubah arah-nya dan mengitari sisi / pojokan penghalang. |
| − | Perlu di catat bahwa difraksi akan membebani daya, energy dari gelombang yang terdifraksi akan sangat jauh lebih kecil dari barisan gelombang asal-nya. Pada aplikasi yang sangat spesifik, kita dapat mengambil keuntungan dari difraksi untuk mengatasi hambatan. | + | Perlu di catat bahwa [[difraksi]] akan membebani daya, energy dari gelombang yang terdifraksi akan sangat jauh lebih kecil dari barisan gelombang asal-nya. Pada aplikasi yang sangat spesifik, kita dapat mengambil keuntungan dari [[difraksi]] untuk mengatasi hambatan. |
| Line 35: | Line 35: | ||
** [[WNDW: Menghitung dengan dB | Menghitung dengan dB]] | ** [[WNDW: Menghitung dengan dB | Menghitung dengan dB]] | ||
** [[WNDW: Fisika dalam dunia nyata | Fisika dalam dunia nyata]] | ** [[WNDW: Fisika dalam dunia nyata | Fisika dalam dunia nyata]] | ||
| + | |||
| + | == Headline text == | ||
Latest revision as of 13:11, 11 September 2009
Difraksi akan tampak seperti pembelokan dari gelombang pada saat menabrak sebuah objek. Hal ini merupakan efek dari “gelombang akan mengitari pojokan”.
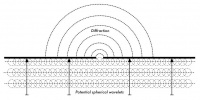
Bayangkan sebuah gelombang di air merambat dalam barisan gelombang yang lurus, seperti barisan gelombang yang sering kita lihat di pantai. Bayangkan jika kita meletakan penghalang benda padat, misalnya pagar kayu yang rapat, yang menghalangi pergerakan gelobang. Jika kita memotong pagar tersebut, dan membuat bukaan sempit di pagar, seperti sebuah pintu yang kecil. Dari bukaan tersebut, sebuah gelombang sirkular akan di mulai, dan akan merambat ke berbagai tempat yang tidak garis lurus dari pembukaan yang kita buat, tapi juga ke lokasi-lokasi yang ada di samping pembukaan. Jika kita melihat barisan gelombang – yang mungkin saja berupa gelombang elektromagnetik – sebagai sinar yang lurus, akan susah untuk menerangkan bagaimana caranya mencapai titik-titik yang tersembunyi di balik penghalang. Dengan model barisan gelombang, maka fenomena ini menjadi masuk akal.
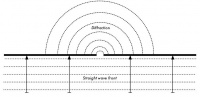
Prinsip Huygens memberikan sebuah model untuk mengerti perilaku ini. Bayangkan pada saat tertentu, semua titik di barisan gelombang menjadi titik awal dari gelombang kecil yang menyebar. Ide ini kemudian di kembangkan oleh Fresnel, apakah hal ini cukup untuk menjelaskan fenomena yang terjadi memang masih menjadi perdebatan. Akan tetapi untuk kebutuhan kita, model Huygens dapat menjelaskan effek yang terjadi dengan cukup baik.
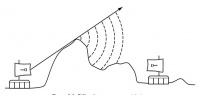
Melalui kemampuan untuk difraksi, gelombang akan “membelok” melewati pojokan atau melalui pembukaan kecil yang ada di penghalang. Untuk panjang gelombang cahaya biasanya terlalu kecil untuk manusia untuk melihat efek ini secara langsung. Pada gelombang mikro, dimana panjang gelombangnya beberapa centimeter, akan menampakan efek difraksi saat gelombang menabrak tembok, puncak gunung, dan berbagai halangan lainnya. Tampaknya seperti penghalang akan menyebabkan gelombang mengubah arah-nya dan mengitari sisi / pojokan penghalang.
Perlu di catat bahwa difraksi akan membebani daya, energy dari gelombang yang terdifraksi akan sangat jauh lebih kecil dari barisan gelombang asal-nya. Pada aplikasi yang sangat spesifik, kita dapat mengambil keuntungan dari difraksi untuk mengatasi hambatan.
Pranala Menarik
- WNDW
- Pengenalan Praktis Tentang Fisika Radio
- Apakah gelombang?
- Kekuatan Elektromagnetik
- Pangkat sepuluhan
- Polarisasi
- Spektrum Elektromagnetik
- Bandwidth
- Frekuensi dan Kanal
- Perilaku Gelombang Radio
- Absorsi / Penyerapan
- Refleksi / Pantulan
- Difraksi
- Interferensi
- Line of sight
- Memahami Fresnel zone
- Daya
- Menghitung dengan dB
- Fisika dalam dunia nyata