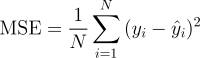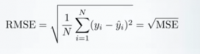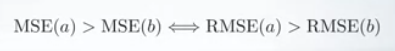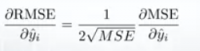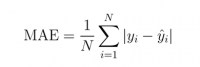Difference between revisions of "Orange: Metric Evaluation Model"
Onnowpurbo (talk | contribs) (Created page with "Sumber: https://towardsdatascience.com/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0 Each machine learning m...") |
(No difference)
|
Revision as of 05:27, 11 July 2019
Each machine learning model is trying to solve a problem with a different objective using a different dataset and hence, it is important to understand the context before choosing a metric. Usually, the answers to the following question help us choose the appropriate metric:
Type of task: Regression? Classification? Business goal? What is the distribution of the target variable?
Well, in this post, I will be discussing the usefulness of each error metric depending on the objective and the problem we are trying to solve. Part1 focuses only to the regression evaluation metrics. Andros island in Greece
Regression Metrics
Mean Squared Error (MSE) Root Mean Squared Error (RMSE) Mean Absolute Error (MAE) R Squared (R²) Adjusted R Squared (R²) Mean Square Percentage Error (MSPE) Mean Absolute Percentage Error (MAPE) Root Mean Squared Logarithmic Error (RMSLE)
Mean Squared Error (MSE)
It is perhaps the most simple and common metric for regression evaluation, but also probably the least useful. It is defined by the equation
where yᵢ is the actual expected output and ŷᵢ is the model’s prediction.
MSE basically measures average squared error of our predictions. For each point, it calculates square difference between the predictions and the target and then average those values.
The higher this value, the worse the model is. It is never negative, since we’re squaring the individual prediction-wise errors before summing them, but would be zero for a perfect model .
Advantage: Useful if we have unexpected values that we should care about. Vey high or low value that we should pay attention.
Disadvantage: If we make a single very bad prediction, the squaring will make the error even worse and it may skew the metric towards overestimating the model’s badness. That is a particularly problematic behaviour if we have noisy data (that is, data that for whatever reason is not entirely reliable) — even a “perfect” model may have a high MSE in that situation, so it becomes hard to judge how well the model is performing. On the other hand, if all the errors are small, or rather, smaller than 1, than the opposite effect is felt: we may underestimate the model’s badness.
Note that if we want to have a constant prediction the best one will be the mean value of the target values. It can be found by setting the derivative of our total error with respect to that constant to zero, and find it from this equation.
Root Mean Squared Error (RMSE)
RMSE is just the square root of MSE. The square root is introduced to make scale of the errors to be the same as the scale of targets.
Now, it is very important to understand in what sense RMSE is similar to MSE,and what is the difference.
First, they are similar in terms of their minimizers, every minimizer of MSE is also a minimizer for RMSE and vice versa since the square root is an non-decreasing function. For example, if we have two sets of predictions, A and B, and say MSE of A is greater than MSE of B, then we can be sure that RMSE of A is greater RMSE of B.And it also works in the opposite direction.
What does it mean for us?
It means that, if the target metric is RMSE, we still can compare our models using MSE,since MSE will order the models in the same way as RMSE. Thus we can optimize MSE instead of RMSE.
In fact, MSE is a little bit easier to work with, so everybody uses MSE instead of RMSE. Also a little bit of difference between the two for gradient-based models.
Gradient of RMSE with respect to i-th prediction
It means that travelling along MSE gradient is equivalent to traveling along RMSE gradient but with a different flowing rate and the flowing rate depends on MSE score itself.
So even though RMSE and MSE are really similar in terms of models scoring, they can be not immediately interchangeable for gradient based methods. We will probably need to adjust some parameters like the learning rate.
Mean Absolute Error (MAE)
In MAE the error is calculated as an average of absolute differences between the target values and the predictions. The MAE is a linear score which means that all the individual differences are weighted equally in the average. For example, the difference between 10 and 0 will be twice the difference between 5 and 0. However, same is not true for RMSE. Mathematically, it is calculated using this formula:
What is important about this metric is that it penalizes huge errors that not as that badly as MSE does. Thus, it’s not that sensitive to outliers as mean square error.
MAE is widely used in finance, where $10 error is usually exactly two times worse than $5 error. On the other hand, MSE metric thinks that $10 error is four times worse than $5 error. MAE is easier to justify than RMSE.
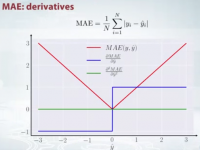
Another important thing about MAE is its gradients with respect to the predictions.The gradiend is a step function and it takes -1 when Y_hat is smaller than the target and +1 when it is larger.
Now, the gradient is not defined when the prediction is perfect,because when Y_hat is equal to Y, we can not evaluate gradient. It is not defined.
So formally, MAE is not differentiable, but in fact, how often your predictions perfectly measure the target. Even if they do, we can write a simple IF condition and returnzero when it is the case and through gradient otherwise. Also know that second derivative is zero everywhere and not defined in the point zero.
Note that if we want to have a constant prediction the best one will be the median value of the target values. It can be found by setting the derivative of our total error with respect to that constant to zero, and find it from this equation.
R Squared (R²)
Now, what if I told you that MSE for my models predictions is 32? Should I improve my model or is it good enough?Or what if my MSE was 0.4?Actually, it’s hard to realize if our model is good or not by looking at the absolute values of MSE or RMSE.We would probably want to measure how much our model is better than the constant baseline.
The coefficient of determination, or R² (sometimes read as R-two), is another metric we may use to evaluate a model and it is closely related to MSE, but has the advantage of being scale-free — it doesn’t matter if the output values are very large or very small, the R² is always going to be between -∞ and 1.
When R² is negative it means that the model is worse than predicting the mean.
The MSE of the model is computed as above, while the MSE of the baseline is defined as:
where the y with a bar is the mean of the observed yᵢ.
To make it more clear, this baseline MSE can be thought of as the MSE that the simplest possible model would get. The simplest possible model would be to always predict the average of all samples. A value close to 1 indicates a model with close to zero error, and a value close to zero indicates a model very close to the baseline.
In conclusion, R² is the ratio between how good our model is vs how good is the naive mean model.
Common Misconception: Alot of articles in the web states that the range of R² lies between 0 and 1 which is not actually true. The maximum value of R² is 1 but minimum can be minus infinity.
For example, consider a really crappy model predicting highly negative value for all the observations even though y_actual is positive. In this case, R² will be less than 0. This is a highly unlikely scenario but the possibility still exists.
MAE vs MSE
I stated that MAE is more robust (less sensitive to outliers) than MSE but this doesn’t mean it is always better to use MAE. The following questions help you to decide:
Take-home message
In this article, we discussed several important regression metrics. We first discussed, Mean Square Error and realized that the best constant for it is the mean targeted value. Root Mean Square Error, and R² are very similar to MSE from optimization perspective. We then discussed Mean Absolute Error and when people prefer to use MAE over MSE.