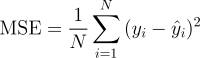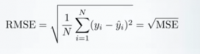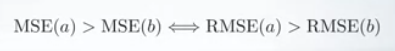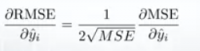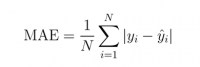Difference between revisions of "Orange: Metric Evaluation Model"
Onnowpurbo (talk | contribs) |
Onnowpurbo (talk | contribs) |
||
| Line 60: | Line 60: | ||
Gradien RMSE sehubungan dengan prediksi ke-i | Gradien RMSE sehubungan dengan prediksi ke-i | ||
| − | + | Ini berarti bahwa perjalanan sepanjang MSE gradient sama dengan perjalanan di sepanjang RMSE gradient tetapi dengan laju aliran yang berbeda dan laju aliran tergantung pada skor MSE itu sendiri. | |
| − | + | Jadi meskipun RMSE dan MSE benar-benar mirip dalam hal penilaian model, mereka tidak dapat segera dipertukarkan untuk metode berbasis gradien. Kita mungkin perlu menyesuaikan beberapa parameter seperti learning rate. | |
==Mean Absolute Error (MAE)== | ==Mean Absolute Error (MAE)== | ||
Revision as of 13:53, 28 January 2020
Setiap machine learning model sedang mencoba untuk memecahkan masalah dengan tujuan yang berbeda menggunakan dataset yang berbeda dan karenanya, penting untuk memahami konteksnya sebelum memilih metrik. Biasanya, jawaban atas pertanyaan berikut membantu kita memilih metrik yang sesuai:
- Jenis tugas: Regressi? Klassifikasi?
- Business goal?
- Seperti apa distribusi variabel target?
Metrik Regressi
Mean Squared Error (MSE) Root Mean Squared Error (RMSE) Mean Absolute Error (MAE) R Squared (R²) Adjusted R Squared (R²) Mean Square Percentage Error (MSPE) Mean Absolute Percentage Error (MAPE) Root Mean Squared Logarithmic Error (RMSLE)
Mean Squared Error (MSE)
Ini mungkin merupakan metrik paling sederhana dan umum untuk evaluasi regresi, tetapi juga mungkin yang paling tidak berguna. Ini didefinisikan oleh persamaan
dimana yᵢ adalah output aktual yang diharapkan dan ŷᵢ adalah prediksi model.
MSE pada dasarnya mengukur kesalahan kuadrat rata-rata dari prediksi kita. Untuk setiap poin, ia menghitung selisih kuadrat antara prediksi dan target kemudian merata-rata nilai-nilai itu.
Semakin tinggi nilai ini, semakin buruk modelnya. Nilai MSE tidak pernah negatif, karena kita menguadratkan kesalahan prediksi individu sebelum menjumlahkannya, tetapi akan menjadi nol untuk model yang sempurna.
Keuntungan: Berguna jika kita memiliki nilai tak terduga yang harus kita pedulikan. Nilai sangat tinggi atau rendah yang harus kita perhatikan.
Kerugian: Jika kita membuat satu prediksi yang sangat buruk, kuadrat akan membuat kesalahan lebih buruk dan itu mungkin membuat metrik cenderung melebih-lebihkan keburukan model. Itu adalah perilaku yang sangat bermasalah jika kita memiliki data yang noisy (yaitu, data yang karena alasan apa pun tidak sepenuhnya dapat diandalkan) - bahkan model "sempurna" mungkin memiliki MSE tinggi dalam situasi itu, sehingga menjadi sulit untuk menilai seberapa baik model sedang melakukan. Di sisi lain, jika semua kesalahan kecil, atau lebih tepatnya, lebih kecil dari 1, dari efek sebaliknya dirasakan: kita dapat meremehkan keburukan model.
Sebagai catatan bahwa jika kita ingin memiliki prediksi konstan, yang terbaik adalah nilai rata-rata dari nilai target. Ini dapat ditemukan dengan menetapkan turunan dari kesalahan total kita sehubungan dengan konstanta ke nol, dan menemukannya dari persamaan ini.
Root Mean Squared Error (RMSE)
RMSE hanya akar kuadrat dari MSE. Root kuadrat diperkenalkan untuk membuat skala kesalahan menjadi sama dengan skala target.
Sekarang, sangat penting untuk memahami dalam hal apa RMSE mirip dengan MSE, jadi apa bedanya.
Pertama, RMSE mirip dalam hal yang mereka minimum-kan, setiap minimizer MSE juga merupakan minimizer untuk RMSE dan sebaliknya karena akar kuadrat adalah fungsi yang tidak menurun. Misalnya, jika kita memiliki dua set prediksi, A dan B, dan katakanlah MSE dari A lebih besar daripada MSE dari B, maka kita dapat yakin bahwa RMSE dari A adalah RMSE yang lebih besar dari B. Dan hal itu juga berlaku untuk arah yang berlawanan.
Apa arti-nya bagi kita?
Ini berarti bahwa, jika metrik target adalah RMSE, kita masih dapat membandingkan model kita yang menggunakan MSE, karena MSE akan memberi perintah model dengan cara yang sama seperti RMSE. Dengan demikian kita dapat mengoptimalkan MSE daripada RMSE.
Faktanya, MSE sedikit lebih mudah untuk dikerjakan, jadi semua orang menggunakan MSE daripada RMSE. Juga sedikit perbedaan antara keduanya untuk model berbasis gradien.
Gradien RMSE sehubungan dengan prediksi ke-i
Ini berarti bahwa perjalanan sepanjang MSE gradient sama dengan perjalanan di sepanjang RMSE gradient tetapi dengan laju aliran yang berbeda dan laju aliran tergantung pada skor MSE itu sendiri.
Jadi meskipun RMSE dan MSE benar-benar mirip dalam hal penilaian model, mereka tidak dapat segera dipertukarkan untuk metode berbasis gradien. Kita mungkin perlu menyesuaikan beberapa parameter seperti learning rate.
Mean Absolute Error (MAE)
In MAE the error is calculated as an average of absolute differences between the target values and the predictions. The MAE is a linear score which means that all the individual differences are weighted equally in the average. For example, the difference between 10 and 0 will be twice the difference between 5 and 0. However, same is not true for RMSE. Mathematically, it is calculated using this formula:
What is important about this metric is that it penalizes huge errors that not as that badly as MSE does. Thus, it’s not that sensitive to outliers as mean square error.
MAE is widely used in finance, where $10 error is usually exactly two times worse than $5 error. On the other hand, MSE metric thinks that $10 error is four times worse than $5 error. MAE is easier to justify than RMSE.
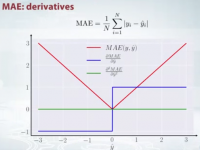
Another important thing about MAE is its gradients with respect to the predictions.The gradiend is a step function and it takes -1 when Y_hat is smaller than the target and +1 when it is larger.
Now, the gradient is not defined when the prediction is perfect,because when Y_hat is equal to Y, we can not evaluate gradient. It is not defined.
So formally, MAE is not differentiable, but in fact, how often your predictions perfectly measure the target. Even if they do, we can write a simple IF condition and returnzero when it is the case and through gradient otherwise. Also know that second derivative is zero everywhere and not defined in the point zero.
Note that if we want to have a constant prediction the best one will be the median value of the target values. It can be found by setting the derivative of our total error with respect to that constant to zero, and find it from this equation.
R Squared (R²)
Now, what if I told you that MSE for my models predictions is 32? Should I improve my model or is it good enough?Or what if my MSE was 0.4?Actually, it’s hard to realize if our model is good or not by looking at the absolute values of MSE or RMSE.We would probably want to measure how much our model is better than the constant baseline.
The coefficient of determination, or R² (sometimes read as R-two), is another metric we may use to evaluate a model and it is closely related to MSE, but has the advantage of being scale-free — it doesn’t matter if the output values are very large or very small, the R² is always going to be between -∞ and 1.
When R² is negative it means that the model is worse than predicting the mean.
The MSE of the model is computed as above, while the MSE of the baseline is defined as:
where the y with a bar is the mean of the observed yᵢ.
To make it more clear, this baseline MSE can be thought of as the MSE that the simplest possible model would get. The simplest possible model would be to always predict the average of all samples. A value close to 1 indicates a model with close to zero error, and a value close to zero indicates a model very close to the baseline.
In conclusion, R² is the ratio between how good our model is vs how good is the naive mean model.
Common Misconception: Alot of articles in the web states that the range of R² lies between 0 and 1 which is not actually true. The maximum value of R² is 1 but minimum can be minus infinity.
For example, consider a really crappy model predicting highly negative value for all the observations even though y_actual is positive. In this case, R² will be less than 0. This is a highly unlikely scenario but the possibility still exists.
MAE vs MSE
I stated that MAE is more robust (less sensitive to outliers) than MSE but this doesn’t mean it is always better to use MAE. The following questions help you to decide:
Take-home message
In this article, we discussed several important regression metrics. We first discussed, Mean Square Error and realized that the best constant for it is the mean targeted value. Root Mean Square Error, and R² are very similar to MSE from optimization perspective. We then discussed Mean Absolute Error and when people prefer to use MAE over MSE.