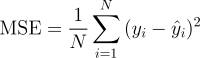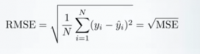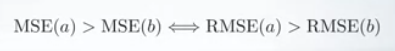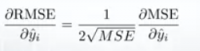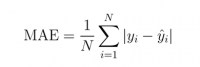Difference between revisions of "Orange: Metric Evaluation Model"

Latest revision as of 07:27, 29 January 2020

Sumber: https://towardsdatascience.com/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0

Setiap machine learning model sedang mencoba untuk memecahkan masalah dengan tujuan yang berbeda menggunakan dataset yang berbeda dan karenanya, penting untuk memahami konteksnya sebelum memilih metrik. Biasanya, jawaban atas pertanyaan berikut membantu kita memilih metrik yang sesuai:

Jenis tugas: Regressi? Klassifikasi?
Business goal?
Seperti apa distribusi variabel target?

Metrik Regressi

Mean Squared Error (MSE)
Root Mean Squared Error (RMSE)
Mean Absolute Error (MAE)
R Squared (R²)
Adjusted R Squared (R²)
Mean Square Percentage Error (MSPE)
Mean Absolute Percentage Error (MAPE)
Root Mean Squared Logarithmic Error (RMSLE)

Mean Squared Error (MSE)

Ini mungkin merupakan metrik paling sederhana dan umum untuk evaluasi regresi, tetapi juga mungkin yang paling tidak berguna. Ini didefinisikan oleh persamaan

dimana yᵢ adalah output aktual yang diharapkan dan ŷᵢ adalah prediksi model.

MSE pada dasarnya mengukur kesalahan kuadrat rata-rata dari prediksi kita. Untuk setiap poin, ia menghitung selisih kuadrat antara prediksi dan target kemudian merata-rata nilai-nilai itu.

Semakin tinggi nilai ini, semakin buruk modelnya. Nilai MSE tidak pernah negatif, karena kita menguadratkan kesalahan prediksi individu sebelum menjumlahkannya, tetapi akan menjadi nol untuk model yang sempurna.

Keuntungan: Berguna jika kita memiliki nilai tak terduga yang harus kita pedulikan. Nilai sangat tinggi atau rendah yang harus kita perhatikan.

Kerugian: Jika kita membuat satu prediksi yang sangat buruk, kuadrat akan membuat kesalahan lebih buruk dan itu mungkin membuat metrik cenderung melebih-lebihkan keburukan model. Itu adalah perilaku yang sangat bermasalah jika kita memiliki data yang noisy (yaitu, data yang karena alasan apa pun tidak sepenuhnya dapat diandalkan) - bahkan model "sempurna" mungkin memiliki MSE tinggi dalam situasi itu, sehingga menjadi sulit untuk menilai seberapa baik model sedang melakukan. Di sisi lain, jika semua kesalahan kecil, atau lebih tepatnya, lebih kecil dari 1, dari efek sebaliknya dirasakan: kita dapat meremehkan keburukan model.

Sebagai catatan bahwa jika kita ingin memiliki prediksi konstan, yang terbaik adalah nilai rata-rata dari nilai target. Ini dapat ditemukan dengan menetapkan turunan dari kesalahan total kita sehubungan dengan konstanta ke nol, dan menemukannya dari persamaan ini.

Root Mean Squared Error (RMSE)

RMSE hanya akar kuadrat dari MSE. Root kuadrat diperkenalkan untuk membuat skala kesalahan menjadi sama dengan skala target.

Sekarang, sangat penting untuk memahami dalam hal apa RMSE mirip dengan MSE, jadi apa bedanya.

Pertama, RMSE mirip dalam hal yang mereka minimum-kan, setiap minimizer MSE juga merupakan minimizer untuk RMSE dan sebaliknya karena akar kuadrat adalah fungsi yang tidak menurun. Misalnya, jika kita memiliki dua set prediksi, A dan B, dan katakanlah MSE dari A lebih besar daripada MSE dari B, maka kita dapat yakin bahwa RMSE dari A adalah RMSE yang lebih besar dari B. Dan hal itu juga berlaku untuk arah yang berlawanan.

Apa arti-nya bagi kita?

Ini berarti bahwa, jika metrik target adalah RMSE, kita masih dapat membandingkan model kita yang menggunakan MSE, karena MSE akan memberi perintah model dengan cara yang sama seperti RMSE. Dengan demikian kita dapat mengoptimalkan MSE daripada RMSE.

Faktanya, MSE sedikit lebih mudah untuk dikerjakan, jadi semua orang menggunakan MSE daripada RMSE. Juga sedikit perbedaan antara keduanya untuk model berbasis gradien.

Gradien RMSE sehubungan dengan prediksi ke-i

Ini berarti bahwa perjalanan sepanjang MSE gradient sama dengan perjalanan di sepanjang RMSE gradient tetapi dengan laju aliran yang berbeda dan laju aliran tergantung pada skor MSE itu sendiri.

Jadi meskipun RMSE dan MSE benar-benar mirip dalam hal penilaian model, mereka tidak dapat segera dipertukarkan untuk metode berbasis gradien. Kita mungkin perlu menyesuaikan beberapa parameter seperti learning rate.

Mean Absolute Error (MAE)

Dalam MAE kesalahan dihitung sebagai rata-rata perbedaan absolut antara nilai target dan prediksi. MAE adalah skor linier yang berarti bahwa semua perbedaan individu diberi bobot yang sama rata-rata. Misalnya, perbedaan antara 10 dan 0 akan menjadi dua kali perbedaan antara 5 dan 0. Namun, hal yang sama tidak berlaku untuk RMSE. Secara matematis, dihitung menggunakan rumus ini:

Yang penting tentang metrik ini adalah metrik ini menghukum kesalahan besar yang tidak separah MSE. Dengan demikian, itu tidak sensitif terhadap outlier sebagai kesalahan kuadrat rata-rata.

MAE banyak digunakan dalam keuangan, di mana kesalahan $10 biasanya dua kali lebih buruk daripada kesalahan $5. Di sisi lain, metrik MSE berpikir bahwa kesalahan $10 adalah empat kali lebih buruk daripada kesalahan $5. MAE lebih mudah di justifikasi daripada RMSE.

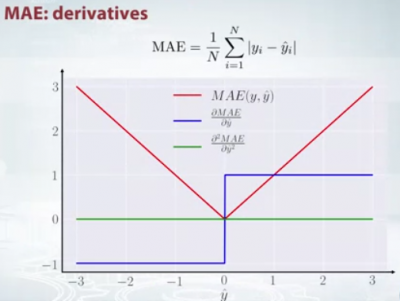
Hal penting lainnya tentang MAE adalah gradiennya sehubungan dengan prediksi. Gradien adalah fungsi langkah dan dibutuhkan -1 saat Y_hat lebih kecil dari target dan +1 saat lebih besar.

Sekarang, gradien tidak didefinisikan ketika prediksi sempurna, karena ketika Y_hat sama dengan Y, kita tidak dapat mengevaluasi gradien. Itu tidak didefinisikan.

Jadi secara formal, MAE tidak dapat dibedakan, tetapi pada kenyataannya, seberapa sering prediksi mereka mengukur target dengan sempurna. Bahkan jika mereka melakukannya, kita dapat menulis kondisi IF sederhana dan returnzero ketika itu terjadi dan melalui gradien sebaliknya. Ketahuilah juga bahwa turunan kedua adalah nol di mana-mana dan tidak didefinisikan di titik nol.

Perhatikan bahwa jika kita ingin memiliki prediksi konstan, yang terbaik adalah nilai median dari nilai target. Ini dapat ditemukan dengan menetapkan turunan dari kesalahan total kita sehubungan dengan konstanta ke nol, dan menemukannya dari persamaan ini.

R Squared (R²)

Sekarang, bagaimana jika saya memberi tahu anda bahwa MSE untuk prediksi model saya adalah 32? Haruskah saya meningkatkan model saya atau cukup baik? Atau bagaimana jika MSE saya adalah 0,4? Sebenarnya, sulit untuk menyadari apakah model kita baik atau tidak dengan melihat nilai absolut MSE atau RMSE. Kita mungkin ingin mengukur seberapa banyak model kami lebih baik daripada baseline konstan.

Coefficient of determination, atau R² (atau di kenal sebagai R-two), adalah metric lainyang bisa kita gunakan untyk mengevaluasi sebuah model dan ini berhubungan cukup dekat dengan MSE, tetapi memiliki keuntungan karena bebas skala - tidak masalah jika nilai output sangat besar atau sangat kecil, R² akan selalu berada di antara -∞ and 1.

Ketika R² negatif, artinya model lebih buruk daripada memprediksi rata-rata.

MSE dari model dihitung seperti di atas, sedangkan MSE dari baseline didefinisikan sebagai:

di mana y dengan bar adalah rata-rata yᵢ yang diamati.

Untuk membuatnya lebih jelas, MSE dasar ini dapat dianggap sebagai MSE yang model paling sederhana mungkin dapatkan. Model yang paling sederhana adalah dengan selalu memprediksi rata-rata semua sampel. Nilai mendekati 1 menunjukkan model dengan kesalahan hampir nol, dan nilai mendekati nol menunjukkan model yang sangat dekat dengan baseline.

Kesimpulannya, R² adalah rasio antara seberapa baik model kami vs seberapa baik adalah model rata-rata naif.

Kesalahpahaman umum: Banyak artikel di web menyatakan bahwa kisaran R² terletak antara 0 dan 1 yang sebenarnya tidak benar. Nilai maksimum R² adalah 1 tetapi minimum bisa minus tak terhingga.

Sebagai contoh, pertimbangkan model yang benar-benar jelek yang memprediksi nilai sangat negatif untuk semua pengamatan meskipun y_actual positif. Dalam hal ini, R² akan kurang dari 0. Ini adalah skenario yang sangat tidak mungkin tetapi kemungkinan masih ada.

MAE vs MSE

Biasanya MAE lebih robust (kurang sensitif terhadap outlier) daripada MSE tetapi ini tidak berarti selalu lebih baik menggunakan MAE. Pertanyaan-pertanyaan berikut membantu kita untuk memutuskan:

Kesimpulan

Dalam artikel ini, kita membahas beberapa metrik regresi penting. Kita pertama kali membahas, Mean Square Error dan menyadari bahwa konstanta terbaik untuk itu adalah nilai target rata-rata. Root Mean Square Error, dan R² sangat mirip dengan MSE dari perspektif optimasi. Kami kemudian mendiskusikan Mean Absolute Error dan kapan orang lebih suka menggunakan MAE daripada MSE.

Referensi

https://towardsdatascience.com/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0

@@ Line 34: / Line 34: @@
 Keuntungan: Berguna jika kita memiliki nilai tak terduga yang harus kita pedulikan. Nilai sangat tinggi atau rendah yang harus kita perhatikan.
-Disadvantage: If we make a single very bad prediction, the squaring will make the error even worse and it may skew the metric towards overestimating the model’s badness. That is a particularly problematic behaviour if we have noisy data (that is, data that for whatever reason is not entirely reliable) — even a “perfect” model may have a high MSE in that situation, so it becomes hard to judge how well the model is performing. On the other hand, if all the errors are small, or rather, smaller than 1, than the opposite effect is felt: we may underestimate the model’s badness.
+Kerugian: Jika kita membuat satu prediksi yang sangat buruk, kuadrat akan membuat kesalahan lebih buruk dan itu mungkin membuat metrik cenderung melebih-lebihkan keburukan model. Itu adalah perilaku yang sangat bermasalah jika kita memiliki data yang noisy (yaitu, data yang karena alasan apa pun tidak sepenuhnya dapat diandalkan) - bahkan model "sempurna" mungkin memiliki MSE tinggi dalam situasi itu, sehingga menjadi sulit untuk menilai seberapa baik model sedang melakukan. Di sisi lain, jika semua kesalahan kecil, atau lebih tepatnya, lebih kecil dari 1, dari efek sebaliknya dirasakan: kita dapat meremehkan keburukan model.
-Note that if we want to have a constant prediction the best one will be the mean value of the target values. It can be found by setting the derivative of our total error with respect to that constant to zero, and find it from this equation.
+Sebagai catatan bahwa jika kita ingin memiliki prediksi konstan, yang terbaik adalah nilai rata-rata dari nilai target. Ini dapat ditemukan dengan menetapkan turunan dari kesalahan total kita sehubungan dengan konstanta ke nol, dan menemukannya dari persamaan ini.
 ==Root Mean Squared Error (RMSE)==
-RMSE is just the square root of MSE. The square root is introduced to make scale of the errors to be the same as the scale of targets.
+RMSE hanya akar kuadrat dari MSE. Root kuadrat diperkenalkan untuk membuat skala kesalahan menjadi sama dengan skala target.
 [[File:Metric2.png|center|200px|thumb]]
-Now, it is very important to understand in what sense RMSE is similar to MSE,and what is the difference.
+Sekarang, sangat penting untuk memahami dalam hal apa RMSE mirip dengan MSE, jadi apa bedanya.
-First, they are similar in terms of their minimizers, every minimizer of MSE is also a minimizer for RMSE and vice versa since the square root is an non-decreasing function. For example, if we have two sets of predictions, A and B, and say MSE of A is greater than MSE of B, then we can be sure that RMSE of A is greater RMSE of B.And it also works in the opposite direction.
+Pertama, RMSE mirip dalam hal yang mereka minimum-kan, setiap minimizer MSE juga merupakan minimizer untuk RMSE dan sebaliknya karena akar kuadrat adalah fungsi yang tidak menurun. Misalnya, jika kita memiliki dua set prediksi, A dan B, dan katakanlah MSE dari A lebih besar daripada MSE dari B, maka kita dapat yakin bahwa RMSE dari A adalah RMSE yang lebih besar dari B. Dan hal itu juga berlaku untuk arah yang berlawanan.
 [[File:Metric3.png|center|400px|thumb]]
+Apa arti-nya bagi kita?
-What does it mean for us?
+Ini berarti bahwa, jika metrik target adalah RMSE, kita masih dapat membandingkan model kita yang menggunakan MSE, karena MSE akan memberi perintah model dengan cara yang sama seperti RMSE. Dengan demikian kita dapat mengoptimalkan MSE daripada RMSE.
-It means that, if the target metric is RMSE, we still can compare our models using MSE,since MSE will order the models in the same way as RMSE. Thus we can optimize MSE instead of RMSE.
+Faktanya, MSE sedikit lebih mudah untuk dikerjakan, jadi semua orang menggunakan MSE daripada RMSE. Juga sedikit perbedaan antara keduanya untuk model berbasis gradien.
-In fact, MSE is a little bit easier to work with, so everybody uses MSE instead of RMSE. Also a little bit of difference between the two for gradient-based models.
 [[File:Metric4.png|center|200px|thumb]]
-Gradient of RMSE with respect to i-th prediction
+Gradien RMSE sehubungan dengan prediksi ke-i
-It means that travelling along MSE gradient is equivalent to traveling along RMSE gradient but with a different flowing rate and the flowing rate depends on MSE score itself.
+Ini berarti bahwa perjalanan sepanjang MSE gradient sama dengan perjalanan di sepanjang RMSE gradient tetapi dengan laju aliran yang berbeda dan laju aliran tergantung pada skor MSE itu sendiri.
-So even though RMSE and MSE are really similar in terms of models scoring, they can be not immediately interchangeable for gradient based methods. We will probably need to adjust some parameters like the learning rate.
+Jadi meskipun RMSE dan MSE benar-benar mirip dalam hal penilaian model, mereka tidak dapat segera dipertukarkan untuk metode berbasis gradien. Kita mungkin perlu menyesuaikan beberapa parameter seperti learning rate.
 ==Mean Absolute Error (MAE)==
-In MAE the error is calculated as an average of absolute differences between the target values and the predictions. The MAE is a linear score which means that all the individual differences are weighted equally in the average. For example, the difference between 10 and 0 will be twice the difference between 5 and 0. However, same is not true for RMSE. Mathematically, it is calculated using this formula:
+Dalam MAE kesalahan dihitung sebagai rata-rata perbedaan absolut antara nilai target dan prediksi. MAE adalah skor linier yang berarti bahwa semua perbedaan individu diberi bobot yang sama rata-rata. Misalnya, perbedaan antara 10 dan 0 akan menjadi dua kali perbedaan antara 5 dan 0. Namun, hal yang sama tidak berlaku untuk RMSE. Secara matematis, dihitung menggunakan rumus ini:
 [[File:Metric5.png|center|200px|thumb]]
-What is important about this metric is that it penalizes huge errors that not as that badly as MSE does. Thus, it’s not that sensitive to outliers as mean square error.
+Yang penting tentang metrik ini adalah metrik ini menghukum kesalahan besar yang tidak separah MSE. Dengan demikian, itu tidak sensitif terhadap outlier sebagai kesalahan kuadrat rata-rata.
-MAE is widely used in finance, where $10 error is usually exactly two times worse than $5 error. On the other hand, MSE metric thinks that $10 error is four times worse than $5 error. MAE is easier to justify than RMSE.
-Another important thing about MAE is its gradients with respect to the predictions.The gradiend is a step function and it takes -1 when Y_hat is smaller than the target and +1 when it is larger.
+MAE banyak digunakan dalam keuangan, di mana kesalahan $10 biasanya dua kali lebih buruk daripada kesalahan $5. Di sisi lain, metrik MSE berpikir bahwa kesalahan $10 adalah empat kali lebih buruk daripada kesalahan $5. MAE lebih mudah di justifikasi daripada RMSE.
-Now, the gradient is not defined when the prediction is perfect,because when Y_hat is equal to Y, we can not evaluate gradient. It is not defined.
+Hal penting lainnya tentang MAE adalah gradiennya sehubungan dengan prediksi. Gradien adalah fungsi langkah dan dibutuhkan -1 saat Y_hat lebih kecil dari target dan +1 saat lebih besar.
+Sekarang, gradien tidak didefinisikan ketika prediksi sempurna, karena ketika Y_hat sama dengan Y, kita tidak dapat mengevaluasi gradien. Itu tidak didefinisikan.
-[[File:Metric6.png|center|200px|thumb]]
+[[File:Metric6.png|center|400px|thumb]]
-So formally, MAE is not differentiable, but in fact, how often your predictions perfectly measure the target. Even if they do, we can write a simple IF condition and returnzero when it is the case and through gradient otherwise. Also know that second derivative is zero everywhere and not defined in the point zero.
+Jadi secara formal, MAE tidak dapat dibedakan, tetapi pada kenyataannya, seberapa sering prediksi mereka mengukur target dengan sempurna. Bahkan jika mereka melakukannya, kita dapat menulis kondisi IF sederhana dan returnzero ketika itu terjadi dan melalui gradien sebaliknya. Ketahuilah juga bahwa turunan kedua adalah nol di mana-mana dan tidak didefinisikan di titik nol.
-Note that if we want to have a constant prediction the best one will be the median value of the target values. It can be found by setting the derivative of our total error with respect to that constant to zero, and find it from this equation.
+Perhatikan bahwa jika kita ingin memiliki prediksi konstan, yang terbaik adalah nilai median dari nilai target. Ini dapat ditemukan dengan menetapkan turunan dari kesalahan total kita sehubungan dengan konstanta ke nol, dan menemukannya dari persamaan ini.
 ==R Squared (R²)==
-Now, what if I told you that MSE for my models predictions is 32? Should I improve my model or is it good enough?Or what if my MSE was 0.4?Actually, it’s hard to realize if our model is good or not by looking at the absolute values of MSE or RMSE.We would probably want to measure how much our model is better than the constant baseline.
+Sekarang, bagaimana jika saya memberi tahu anda bahwa MSE untuk prediksi model saya adalah 32? Haruskah saya meningkatkan model saya atau cukup baik? Atau bagaimana jika MSE saya adalah 0,4? Sebenarnya, sulit untuk menyadari apakah model kita baik atau tidak dengan melihat nilai absolut MSE atau RMSE. Kita mungkin ingin mengukur seberapa banyak model kami lebih baik daripada baseline konstan.
-The coefficient of determination, or R² (sometimes read as R-two), is another metric we may use to evaluate a model and it is closely related to MSE, but has the advantage of being scale-free — it doesn’t matter if the output values are very large or very small, the R² is always going to be between -∞ and 1.
+Coefficient of determination, atau R² (atau di kenal sebagai R-two), adalah metric lainyang bisa kita gunakan untyk mengevaluasi sebuah model dan ini berhubungan cukup dekat dengan MSE, tetapi memiliki keuntungan karena bebas skala - tidak masalah jika nilai output sangat besar atau sangat kecil, R² akan selalu berada di antara -∞ and 1.
-When R² is negative it means that the model is worse than predicting the mean.
+Ketika R² negatif, artinya model lebih buruk daripada memprediksi rata-rata.
 [[File:Metric7.png|center|200px|thumb]]
-The MSE of the model is computed as above, while the MSE of the baseline is defined as:
+MSE dari model dihitung seperti di atas, sedangkan MSE dari baseline didefinisikan sebagai:
 [[File:Metric8.png|center|200px|thumb]]
-where the y with a bar is the mean of the observed yᵢ.
+di mana y dengan bar adalah rata-rata yᵢ yang diamati.
-To make it more clear, this baseline MSE can be thought of as the MSE that the simplest possible model would get. The simplest possible model would be to always predict the average of all samples. A value close to 1 indicates a model with close to zero error, and a value close to zero indicates a model very close to the baseline.
+Untuk membuatnya lebih jelas, MSE dasar ini dapat dianggap sebagai MSE yang model paling sederhana mungkin dapatkan. Model yang paling sederhana adalah dengan selalu memprediksi rata-rata semua sampel. Nilai mendekati 1 menunjukkan model dengan kesalahan hampir nol, dan nilai mendekati nol menunjukkan model yang sangat dekat dengan baseline.
-In conclusion, R² is the ratio between how good our model is vs how good is the naive mean model.
+Kesimpulannya, R² adalah rasio antara seberapa baik model kami vs seberapa baik adalah model rata-rata naif.
-Common Misconception: Alot of articles in the web states that the range of R² lies between 0 and 1 which is not actually true. The maximum value of R² is 1 but minimum can be minus infinity.
+Kesalahpahaman umum: Banyak artikel di web menyatakan bahwa kisaran R² terletak antara 0 dan 1 yang sebenarnya tidak benar. Nilai maksimum R² adalah 1 tetapi minimum bisa minus tak terhingga.
-For example, consider a really crappy model predicting highly negative value for all the observations even though y_actual is positive. In this case, R² will be less than 0. This is a highly unlikely scenario but the possibility still exists.
+Sebagai contoh, pertimbangkan model yang benar-benar jelek yang memprediksi nilai sangat negatif untuk semua pengamatan meskipun y_actual positif. Dalam hal ini, R² akan kurang dari 0. Ini adalah skenario yang sangat tidak mungkin tetapi kemungkinan masih ada.
 ==MAE vs MSE==
-I stated that MAE is more robust (less sensitive to outliers) than MSE but this doesn’t mean it is always better to use MAE. The following questions help you to decide:
+Biasanya MAE lebih robust (kurang sensitif terhadap outlier) daripada MSE tetapi ini tidak berarti selalu lebih baik menggunakan MAE. Pertanyaan-pertanyaan berikut membantu kita untuk memutuskan:
 [[File:Metric9.png|center|200px|thumb]]
+==Kesimpulan==
-==Take-home message==
+Dalam artikel ini, kita membahas beberapa metrik regresi penting. Kita pertama kali membahas, Mean Square Error dan menyadari bahwa konstanta terbaik untuk itu adalah nilai target rata-rata. Root Mean Square Error, dan R² sangat mirip dengan MSE dari perspektif optimasi. Kami kemudian mendiskusikan Mean Absolute Error dan kapan orang lebih suka menggunakan MAE daripada MSE.
-In this article, we discussed several important regression metrics. We first discussed, Mean Square Error and realized that the best constant for it is the mean targeted value. Root Mean Square Error, and R² are very similar to MSE from optimization perspective. We then discussed Mean Absolute Error and when people prefer to use MAE over MSE.
+==Referensi==
+* https://towardsdatascience.com/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0
+==Pranala Menarik==
+* [[Data Science]]
+* [[Orange]]
-==Referensi==
-* https://towardsdatascience.com/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0