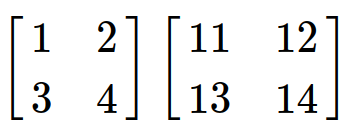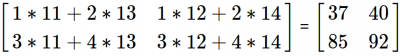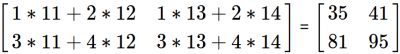Pyhton: NumPy Matrix dan Aljabar Linear

Sumber: http://www.bogotobogo.com/python/python_numpy_matrix_tutorial.php

Apa beda antara numpy dot() and inner()

Mari kita lihat ke 2D array:

import numpy as np
a=np.array([[1,2],[3,4]])
b=np.array([[11,12],[13,14]])

np.dot(a,b)

array([[37, 40],
       [85, 92]])

np.inner(a,b)

array([[35, 41],
       [81, 95]])

NumPy Matrix

Bab-bab tentang NumPy telah menggunakan array (NumPy Array Basics A dan NumPy Array Basics B). Namun, untuk area tertentu seperti aljabar linier, kita mungkin ingin menggunakan matriks.

import numpy as np
A = np.matrix([[1.,2], [3,4], [5,6]])
A

matrix([[ 1.,  2.],
        [ 3.,  4.],
        [ 5.,  6.]])

Kami juga dapat menggunakan gaya Matlab dengan memberikan string bukan list:

import numpy as np
B = np.matrix("1.,2; 3,4; 5,6")
B
matrix([[ 1.,  2.],
        [ 3.,  4.],
        [ 5.,  6.]])

Vector sebagai matrix

Vectors are handled as matrices with one row or one column:

>>> x = np.matrix("10., 20.")
>>> x
matrix(10.,  20.)
>>> x.T
matrix([[ 10.],
        [ 20.]])

Here is an example for matrix and vector multiplication:

>>> x = np.matrix("4.;5.")
>>> x
matrix([[ 4.],
        [ 5.]])

>>> A = np.matrix([[1.,2], [3,4], [5,6]])
>>> A
matrix([[ 1.,  2.],
        [ 3.,  4.],
        [ 5.,  6.]])

>>> A*x
matrix([[ 14.],
        [ 32.],
        [ 50.]])

For vectors, indexing requires two indices:

>>> print x[0,0], x[1,0]
4.0 5.0

Note

Though np.matrix takes a real matrix form and look pleasing, usually, for most of the cases, arrays are good enough.

Rank

>>> import numpy as np
>>> A = np.ones((4,3))
>>> A
array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])
>>> np.rank(A)
2

Note that the rank of the array is not the rank of the matrix in linear algebra (dimension of the column space) but the number of subscripts it takes!

Scalars have rank 0:

>>> x = np.array(10)
>>> x
array(10)
>>> np.rank(x)
0

NumPy supports arrays of any dimension such as rank 3 (2x2x2):

>>> A = np.ones((2,2,2))
>>> A
array([[[ 1.,  1.],
        [ 1.,  1.]], 

       [[ 1.,  1.],
        [ 1.,  1.]]])
>>> A[1,0,1]
1.0

dot product

>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
       [3, 4]])
>>> b = np.array([10, 20])
>>> b
array([10, 20])
>>> ans = np.dot(A,b)
>>> ans
array([ 50, 110])

Ax = b : numpy.linalg

Now we want to solve Ax = b:

>>> import numpy as np
>>> from numpy.linalg import solve
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
       [3, 4]])
>>> b = np.array([10, 20])
>>> b
>>> x = solve(A,b)
>>> x
array([ 0.,  5.])

Eigen Value dan Vector

>>> import numpy as np
>>> from numpy.linalg import eig
>>> A = np.array([[1,2],[3,4]])
>>> eig(A)
(array([-0.37228132,  5.37228132]), array([[-0.82456484, -0.41597356],
       [ 0.56576746, -0.90937671]]))

The eig returns two tuples: the first one is the eigen values and the second one is a matrix whose columns are the two eigen vectors.

We can unpack the tuples:

>>> eigen_val, eigen_vec = eig(A)
>>> eigen_val
array([-0.37228132,  5.37228132])
>>> eigen_vec
array([[-0.82456484, -0.41597356],
       [ 0.56576746, -0.90937671]])

Quadrature

We want to solve ∫30x4dx=2434:

>>> from scipy.integrate import quad
>>> def f(x):
...     return x**4
... 
>>> quad(f, 0., 3.)
(48.599999999999994, 5.39568389967826e-13)

The returned tuple indicates (ans, error estimate).

We can get the same answer if we use lambda instead:

>>> quad(lambda x: x**4, 0, 3)
(48.599999999999994, 5.39568389967826e-13)

Referensi

http://www.bogotobogo.com/python/python_numpy_matrix_tutorial.php