Difference between revisions of "Orange: Stochastic Gradient Descent"
Onnowpurbo (talk | contribs) (Created page with "Sumber: https://docs.biolab.si//3/visual-programming/widgets/model/stochasticgradient.html Minimize an objective function using a stochastic approximation of gradient descen...") |
Onnowpurbo (talk | contribs) |
||
| Line 7: | Line 7: | ||
Data: input dataset | Data: input dataset | ||
| − | |||
Preprocessor: preprocessing method(s) | Preprocessor: preprocessing method(s) | ||
| Line 13: | Line 12: | ||
Learner: stochastic gradient descent learning algorithm | Learner: stochastic gradient descent learning algorithm | ||
| − | |||
Model: trained model | Model: trained model | ||
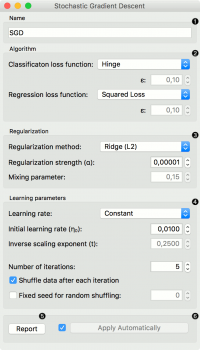
The Stochastic Gradient Descent widget uses stochastic gradient descent that minimizes a chosen loss function with a linear function. The algorithm approximates a true gradient by considering one sample at a time, and simultaneously updates the model based on the gradient of the loss function. For regression, it returns predictors as minimizers of the sum, i.e. M-estimators, and is especially useful for large-scale and sparse datasets. | The Stochastic Gradient Descent widget uses stochastic gradient descent that minimizes a chosen loss function with a linear function. The algorithm approximates a true gradient by considering one sample at a time, and simultaneously updates the model based on the gradient of the loss function. For regression, it returns predictors as minimizers of the sum, i.e. M-estimators, and is especially useful for large-scale and sparse datasets. | ||
| − | + | [[File:StochasticGradientDescent-stamped.png|center|200px|thumb]] | |
Specify the name of the model. The default name is “SGD”. | Specify the name of the model. The default name is “SGD”. | ||
| − | |||
Algorithm parameters: | Algorithm parameters: | ||
| − | |||
Classification loss function: | Classification loss function: | ||
| − | |||
Hinge (linear SVM) | Hinge (linear SVM) | ||
| − | |||
Logistic Regression (logistic regression SGD) | Logistic Regression (logistic regression SGD) | ||
| − | |||
Modified Huber (smooth loss that brings tolerance to outliers as well as probability estimates) | Modified Huber (smooth loss that brings tolerance to outliers as well as probability estimates) | ||
| − | |||
Squared Hinge (quadratically penalized hinge) | Squared Hinge (quadratically penalized hinge) | ||
| − | |||
Perceptron (linear loss used by the perceptron algorithm) | Perceptron (linear loss used by the perceptron algorithm) | ||
| − | |||
Squared Loss (fitted to ordinary least-squares) | Squared Loss (fitted to ordinary least-squares) | ||
| − | |||
Huber (switches to linear loss beyond ε) | Huber (switches to linear loss beyond ε) | ||
| − | |||
Epsilon insensitive (ignores errors within ε, linear beyond it) | Epsilon insensitive (ignores errors within ε, linear beyond it) | ||
| − | |||
Squared epsilon insensitive (loss is squared beyond ε-region). | Squared epsilon insensitive (loss is squared beyond ε-region). | ||
| − | |||
Regression loss function: | Regression loss function: | ||
| − | |||
Squared Loss (fitted to ordinary least-squares) | Squared Loss (fitted to ordinary least-squares) | ||
| − | |||
Huber (switches to linear loss beyond ε) | Huber (switches to linear loss beyond ε) | ||
| − | |||
Epsilon insensitive (ignores errors within ε, linear beyond it) | Epsilon insensitive (ignores errors within ε, linear beyond it) | ||
| − | |||
Squared epsilon insensitive (loss is squared beyond ε-region). | Squared epsilon insensitive (loss is squared beyond ε-region). | ||
| − | |||
Regularization norms to prevent overfitting: | Regularization norms to prevent overfitting: | ||
| − | |||
None. | None. | ||
| − | |||
Lasso (L1) (L1 leading to sparse solutions) | Lasso (L1) (L1 leading to sparse solutions) | ||
| − | |||
Ridge (L2) (L2, standard regularizer) | Ridge (L2) (L2, standard regularizer) | ||
| − | |||
Elastic net (mixing both penalty norms). | Elastic net (mixing both penalty norms). | ||
| − | |||
Regularization strength defines how much regularization will be applied (the less we regularize, the more we allow the model to fit the data) and the mixing parameter what the ratio between L1 and L2 loss will be (if set to 0 then the loss is L2, if set to 1 then it is L1). | Regularization strength defines how much regularization will be applied (the less we regularize, the more we allow the model to fit the data) and the mixing parameter what the ratio between L1 and L2 loss will be (if set to 0 then the loss is L2, if set to 1 then it is L1). | ||
| − | |||
Learning parameters. | Learning parameters. | ||
| − | |||
Learning rate: | Learning rate: | ||
| − | |||
Constant: learning rate stays the same through all epochs (passes) | Constant: learning rate stays the same through all epochs (passes) | ||
| − | |||
Optimal: a heuristic proposed by Leon Bottou | Optimal: a heuristic proposed by Leon Bottou | ||
| − | |||
Inverse scaling: earning rate is inversely related to the number of iterations | Inverse scaling: earning rate is inversely related to the number of iterations | ||
| − | |||
Initial learning rate. | Initial learning rate. | ||
| − | |||
Inverse scaling exponent: learning rate decay. | Inverse scaling exponent: learning rate decay. | ||
| − | |||
Number of iterations: the number of passes through the training data. | Number of iterations: the number of passes through the training data. | ||
| − | |||
If Shuffle data after each iteration is on, the order of data instances is mixed after each pass. | If Shuffle data after each iteration is on, the order of data instances is mixed after each pass. | ||
| − | |||
If Fixed seed for random shuffling is on, the algorithm will use a fixed random seed and enable replicating the results. | If Fixed seed for random shuffling is on, the algorithm will use a fixed random seed and enable replicating the results. | ||
| − | |||
Produce a report. | Produce a report. | ||
| − | |||
Press Apply to commit changes. Alternatively, tick the box on the left side of the Apply button and changes will be communicated automatically. | Press Apply to commit changes. Alternatively, tick the box on the left side of the Apply button and changes will be communicated automatically. | ||
| − | + | ==Contoh== | |
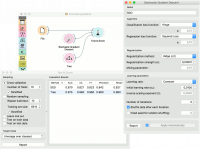
For the classification task, we will use iris dataset and test two models on it. We connected Stochastic Gradient Descent and Tree to Test & Score. We also connected File to Test & Score and observed model performance in the widget. | For the classification task, we will use iris dataset and test two models on it. We connected Stochastic Gradient Descent and Tree to Test & Score. We also connected File to Test & Score and observed model performance in the widget. | ||
| − | + | [[File:StochasticGradientDescent-classification.png|center|200px|thumb]] | |
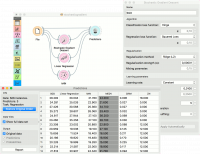
For the regression task, we will compare three different models to see which predict what kind of results. For the purpose of this example, the housing dataset is used. We connect the File widget to Stochastic Gradient Descent, Linear Regression and kNN widget and all four to the Predictions widget. | For the regression task, we will compare three different models to see which predict what kind of results. For the purpose of this example, the housing dataset is used. We connect the File widget to Stochastic Gradient Descent, Linear Regression and kNN widget and all four to the Predictions widget. | ||
| − | + | [[File:StochasticGradientDescent-regression.png|center|200px|thumb]] | |
Revision as of 10:12, 23 January 2020
Sumber: https://docs.biolab.si//3/visual-programming/widgets/model/stochasticgradient.html
Minimize an objective function using a stochastic approximation of gradient descent.
Inputs
Data: input dataset Preprocessor: preprocessing method(s)
Outputs
Learner: stochastic gradient descent learning algorithm Model: trained model
The Stochastic Gradient Descent widget uses stochastic gradient descent that minimizes a chosen loss function with a linear function. The algorithm approximates a true gradient by considering one sample at a time, and simultaneously updates the model based on the gradient of the loss function. For regression, it returns predictors as minimizers of the sum, i.e. M-estimators, and is especially useful for large-scale and sparse datasets.
Specify the name of the model. The default name is “SGD”.
Algorithm parameters:
Classification loss function:
Hinge (linear SVM)
Logistic Regression (logistic regression SGD)
Modified Huber (smooth loss that brings tolerance to outliers as well as probability estimates)
Squared Hinge (quadratically penalized hinge)
Perceptron (linear loss used by the perceptron algorithm)
Squared Loss (fitted to ordinary least-squares)
Huber (switches to linear loss beyond ε)
Epsilon insensitive (ignores errors within ε, linear beyond it)
Squared epsilon insensitive (loss is squared beyond ε-region).
Regression loss function:
Squared Loss (fitted to ordinary least-squares)
Huber (switches to linear loss beyond ε)
Epsilon insensitive (ignores errors within ε, linear beyond it)
Squared epsilon insensitive (loss is squared beyond ε-region).
Regularization norms to prevent overfitting:
None.
Lasso (L1) (L1 leading to sparse solutions)
Ridge (L2) (L2, standard regularizer)
Elastic net (mixing both penalty norms).
Regularization strength defines how much regularization will be applied (the less we regularize, the more we allow the model to fit the data) and the mixing parameter what the ratio between L1 and L2 loss will be (if set to 0 then the loss is L2, if set to 1 then it is L1).
Learning parameters.
Learning rate:
Constant: learning rate stays the same through all epochs (passes)
Optimal: a heuristic proposed by Leon Bottou
Inverse scaling: earning rate is inversely related to the number of iterations
Initial learning rate.
Inverse scaling exponent: learning rate decay.
Number of iterations: the number of passes through the training data.
If Shuffle data after each iteration is on, the order of data instances is mixed after each pass.
If Fixed seed for random shuffling is on, the algorithm will use a fixed random seed and enable replicating the results.
Produce a report.
Press Apply to commit changes. Alternatively, tick the box on the left side of the Apply button and changes will be communicated automatically.
Contoh
For the classification task, we will use iris dataset and test two models on it. We connected Stochastic Gradient Descent and Tree to Test & Score. We also connected File to Test & Score and observed model performance in the widget.
For the regression task, we will compare three different models to see which predict what kind of results. For the purpose of this example, the housing dataset is used. We connect the File widget to Stochastic Gradient Descent, Linear Regression and kNN widget and all four to the Predictions widget.