Difference between revisions of "Keras: Memilih Fungsi Loss"
Onnowpurbo (talk | contribs) |
Onnowpurbo (talk | contribs) |
||
| Line 417: | Line 417: | ||
pyplot.show() | pyplot.show() | ||
| − | + | Menjalankan contoh untuk mem-print akurasi klasifikasi untuk model pada dataset train dan test. | |
| − | + | Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali. | |
In this case, we can see that the model learned the problem reasonably well, achieving about 83% accuracy on the training dataset and about 85% on the test dataset. The scores are reasonably close, suggesting the model is probably not over or underfit. | In this case, we can see that the model learned the problem reasonably well, achieving about 83% accuracy on the training dataset and about 85% on the test dataset. The scores are reasonably close, suggesting the model is probably not over or underfit. | ||
Revision as of 06:22, 30 August 2019
Deep learning neural network di-train dengan menggunakan algoritma stochastic gradient descent optimization.
Sebagai bagian dari optimisasi algoritma, kesalahan kondisi model harus diperkirakan berulang kali. Ini membutuhkan pilihan fungsi kesalahan, secara konvensional disebut fungsi loss, yang dapat digunakan untuk memperkirakan loss model sehingga weight dapat diperbarui untuk mengurangi loss pada evaluasi selanjutnya.
Neural network model mempelajari pemetaan dari input ke output dari contoh dan pilihan fungsi loss harus sesuai dengan framing masalah pemodelan prediktif spesifik, seperti klasifikasi atau regresi. Lebih lanjut, konfigurasi lapisan keluaran juga harus sesuai untuk fungsi loss yang dipilih.
Dalam tutorial ini, kita akan mempelajari cara memilih fungsi loss untuk deep learning neural network untuk masalah pemodelan prediktif yang diberikan.
Sesudah menyelesaikan tutorial ini, anda akan mengetahui:
- Bagaimana mengkonfigurasi model untuk mean squared error dan varian-nya untuk regression problems.
- Bagaimana mengkonfigurasi model untuk cross-entropy dan fungsi hinge loss untuk binary classification.
- Bagaimana mengkonfigurasi model untuk cross-entropy dan fungsi KL divergence loss untuk multi-class classification.
Tutorial Overview
Tutorial ini di bagi dalam tiga bagian, yaitu:
Regression Loss Functions
Mean Squared Error Loss
Mean Squared Logarithmic Error Loss
Mean Absolute Error Loss
Binary Classification Loss Functions
Binary Cross-Entropy
Hinge Loss
Squared Hinge Loss
Multi-Class Classification Loss Functions
Multi-Class Cross-Entropy Loss
Sparse Multiclass Cross-Entropy Loss
Kullback Leibler Divergence Loss
Kita akan fokus pada bagaimana memilih dan mengimplementasikan berbagai fungsi loss. Untuk teori lebih lanjut tentang fungsi loss, bisa lihat tulisan:
Regression Loss Function
Masalah pemodelan prediktif regresi melibatkan memprediksi kuantitas yang bernilai nyata. Pada bagian ini, kita akan menyelidiki fungsi loss yang sesuai untuk masalah pemodelan prediksi regresi.
Sebagai konteks untuk investigasi ini, kami akan menggunakan generator masalah regresi standar yang disediakan oleh perpustakaan scikit-learn di fungsi make_regress(). Fungsi ini akan menghasilkan contoh-contoh dari masalah regresi sederhana dengan sejumlah variabel input, noise statistik, dan properti lainnya.
Kita akan menggunakan fungsi ini untuk mendefinisikan masalah yang memiliki 20 fitur input; 10 fitur bermakna dan 10 tidak relevan. Sebanyak 1.000 contoh akan dihasilkan secara acak. Generator angka pseudorandom akan diperbaiki untuk memastikan bahwa kami mendapatkan 1.000 contoh yang sama setiap kali kode dijalankan.
# generate regression dataset X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
Neural network umumnya berkinerja lebih baik ketika variabel input dan output bernilai real yang di skalakan (scaled) pada kisaran yang masuk akal. Untuk masalah ini, masing-masing variabel input dan variabel target memiliki distribusi Gaussian; oleh karena itu, standarisasi data dalam hal ini dibutuhkan.
Kita dapat mencapai ini menggunakan kelas transformator StandardScaler juga dari library scikit-learn. Pada masalah yang sebenarnya, kita akan menyiapkan scaler pada set data training dan menerapkannya pada set train dan test, tetapi untuk menyederhanakan, kita akan menskalakan semua data bersama sebelum dipecah menjadi set train dan test.
# standardize dataset X = StandardScaler().fit_transform(X) y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
Setelah di skalakan, data dibagi rata menjadi set train dan test.
# split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :]
Model Multilayer Perceptron (MLP) yang kecil akan didefinisikan untuk mengatasi masalah ini dan memberikan dasar untuk mengeksplorasi berbagai fungsi kerugian.
Model akan mengharapkan 20 fitur sebagai input sebagaimana didefinisikan oleh masalah. Model akan memiliki satu lapisan tersembunyi dengan 25 node dan akan menggunakan fungsi rectified linear activation (ReLU). Lapisan output akan memiliki 1 simpul, mengingat satu nilai riil yang akan diprediksi, dan akan menggunakan fungsi aktivasi linier.
# define model model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear'))
Model ini akan cocok dengan stochastic gradient descent dengan learning rate 0,01 dan momentum 0,9, keduanya nilai default yang cukup baik.
Training akan dilakukan sebanyak 100 epoch dan set test akan dievaluasi pada akhir setiap epoch sehingga kita dapat merencanakan kurva learning di akhir run.
opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='...', optimizer=opt) # fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
Sekarang kita memiliki dasar masalah dan model, kita dapat mengevaluasi tiga fungsi loss umum yang sesuai untuk masalah pemodelan prediksi regresi.
Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk regresi.
Mean Squared Error Loss
Mean Squared Error, atau MSE, loss adalah default loss yang digunakan untuk masalah regresi.
Secara matematis, ini adalah fungsi loss yang disukai di bawah inference framework of maximum likelihood jika distribusi variabel target adalah Gaussian. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang bagus.
Mean squared error dihitung sebagai rata-rata perbedaan kuadrat antara nilai yang diprediksi dan yang sebenarnya. Hasilnya selalu positif terlepas dari tanda nilai yang diprediksi dan aktual dan nilai sempurna adalah 0,0. Kuadrat berarti bahwa kesalahan yang lebih besar menghasilkan lebih banyak kesalahan daripada kesalahan yang lebih kecil, yang berarti bahwa model akan dihukum karena membuat kesalahan yang lebih besar.
Fungsi mean squared error loss dapat digunakan dalam Keras dengan menuliskan ‘mse‘ atau ‘mean_squared_error‘ sebagai fungsi loss saat menyusun model.
model.compile(loss='mean_squared_error')
Disarankan bahwa layer output memiliki satu simpul untuk variabel target dan fungsi aktivasi linier digunakan.
model.add(Dense(1, activation='linear'))
Contoh lengkap menunjukkan MLP pada masalah regresi yang dijelaskan tercantum di bawah ini.
# mlp for regression with mse loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_error', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
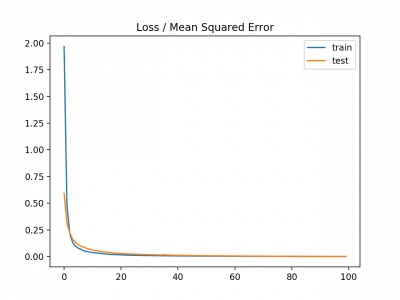
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
Menjalankan contoh pertama mem-print kesalahan kuadrat rata-rata model pada train dan test dataset.
Mengingat sifat stokastik dari algoritma training, Basil spesifik dapat bervariasi. Coba jalankan contoh beberapa kali.
Dalam kasus ini, kita dapat melihat bahwa model berusaha mencapai nol kesalahan, setidaknya sampai tiga tempat desimal.
Train: 0.000, Test: 0.001
Plot garis juga dibuat menunjukkan mean squared error loss selama periode pelatihan untuk set train (biru) dan test (oranye).
Kita dapat melihat bahwa model terkonvergensi dengan cukup cepat dan baik kinerja train dan test tetap setara. Perilaku kinerja dan konvergensi model menunjukkan bahwa mean squared error cocok untuk neural network yang mempelajari masalah ini.
Mean Squared Logarithmic Error Loss
Mungkin ada masalah regresi di mana nilai target memiliki penyebaran nilai dan ketika memprediksi nilai besar, kita mungkin tidak ingin menghukum model sebanyak kesalahan kuadrat rata-rata.
Sebagai gantinya, kita pertama-tama dapat menghitung nilai log dari masing-masing nilai yang diprediksi, lalu menghitung rata-rata kesalahan kuadrat. Ini disebut Mean Squared Logarithmic Error loss, atau disingkat MSLE.
Ini memiliki efek membuat santai efek punishing saat ada perbedaan besar dalam nilai prediksi yang besar.
Sebagai ukuran loss, mungkin lebih tepat ketika model memprediksi unscaled quantities secara langsung. Namun demikian, kita dapat menunjukkan fungsi loss ini menggunakan masalah regresi sederhana.
Model ini dapat diperbarui untuk menggunakan fungsi loss ‘mean_squared_logarithmic_error‘ dan mempertahankan konfigurasi yang sama untuk layer output. Kita juga akan melacak mean squared error sebagai metrik saat memasang model sehingga kita dapat menggunakannya sebagai ukuran kinerja dan plot kurva pembelajaran.
model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
Contoh lengkap menggunakan fungsi loss MSLE tercantum di bawah ini.
# mlp for regression with msle loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()
Menjalankan contoh pertama mem-print mean squared error untuk model pada datset train dan test.
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh tersebut beberapa kali.
Dalam hal ini, kita dapat melihat bahwa model tersebut menghasilkan MSE yang sedikit lebih buruk pada datset training dan testing. Ini mungkin tidak cocok untuk masalah ini karena distribusi variabel target adalah standar Gaussian.
Train: 0.165, Test: 0.184
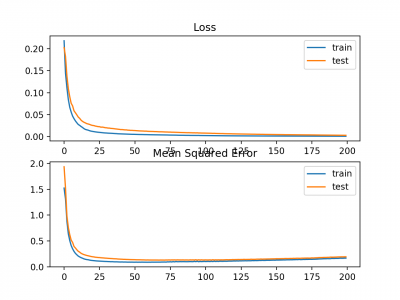
Plot garis juga dibuat menunjukkan mean squared logarithmic error losst selama periode training untuk set train (biru) dan test (oranye) (atas), dan plot yang sama untuk mean squared error (bawah).
Kita dapat melihat bahwa algoritma MSLE konvergen lebih dari a100 epoch; tampaknya MSE mungkin menunjukkan tanda-tanda overfitting dari masalah yang ada, jatuh secara cepat cepat dan mulai naik pada epoch 20 dan seterusnya.
Mean Absolute Error Loss
Pada beberapa masalah regresi, distribusi variabel target mungkin sebagian besar Gaussian, tetapi mungkin memiliki outlier, mis. nilai besar atau kecil jauh dari nilai rata-rata.
The Mean Absolute Error loss, atau MAE, adalah fungsi loss yang sesuai dalam kasus ini karena itu lebih kuat untuk outlier. Ini dihitung sebagai rata-rata perbedaan absolut antara nilai aktual dan prediksi.
Model dapat diperbarui untuk menggunakan fungsi loss ‘mean_absolute_error‘ dan mempertahankan konfigurasi yang sama untuk layer output.
model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
Contoh lengkap menggunakan mean absolute error sebagai fungsi loss pada masalah test regresi terlampir di bawah ini.
# mlp for regression with mae loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()
Menjalankan contoh pertama mem-print mean squared error untuk model dataset train dan test.
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
Dalam kasus ini, kita dapat melihat bahwa model learn masalah, mencapai kesalahan mendekati nol, setidaknya ke tiga tempat desimal.
Train: 0.002, Test: 0.002
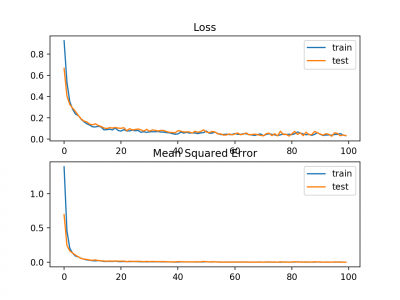
Plot garis juga dibuat yang menunjukkan mean absolute error loss selama periode pelatihan untuk set train (biru) dan test (oranye) (atas), dan plot serupa untuk mean squared error (bawah).
Dalam hal ini, kita dapat melihat bahwa MAE memang konvergen akan tetapi pencapaiannya bergelombang, meskipun dinamika MSE tidak tampak sangat terpengaruh. Kita tahu bahwa variabel target adalah Gaussian standar tanpa outlier besar, sehingga MAE tidak cocok untuk kasus ini.
Mungkin lebih tepat untuk masalah ini jika kita tidak menskalakan variabel target terlebih dahulu.
Binary Classification Loss Function
Klasifikasi biner adalah masalah-masalah pemodelan prediktif di mana contoh diberikan satu dari dua label.
Masalahnya sering di lihat sebagai memprediksi nilai 0 atau 1 untuk kelas pertama atau kedua dan sering diimplementasikan sebagai memprediksi probabilitas milik nilai kelas 1.
Pada bagian ini, kami akan menyelidiki fungsi kerugian yang sesuai untuk masalah pemodelan prediktif klasifikasi biner.
Kami akan menghasilkan contoh dari masalah test lingkaran di scikit-belajar sebagai basis untuk penelitian ini. Masalah lingkaran melibatkan sampel yang diambil dari dua lingkaran konsentris pada bidang dua dimensi, di mana titik pada lingkaran luar milik kelas 0 dan titik untuk lingkaran dalam milik kelas 1. Noise statistik ditambahkan ke sampel untuk menambah ambiguitas dan membuat masalahnya lebih sulit untuk dipelajari.
Kami akan men-generate 1.000 contoh dan menambahkan 10% noise statistik. Generator nomor pseudorandom akan di-seed dengan nilai yang sama untuk memastikan bahwa kami selalu mendapatkan 1.000 contoh yang sama.
# generate circles X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
Kita dapat membuat scatter plot dataset untuk mendapatkan gambaran tentang masalah yang kita modelkan. Contoh lengkapnya tercantum di bawah ini.
# scatter plot of the circles dataset with points colored by class from sklearn.datasets import make_circles from numpy import where from matplotlib import pyplot # generate circles X, y = make_circles(n_samples=1000, noise=0.1, random_state=1) # select indices of points with each class label for i in range(2): samples_ix = where(y == i) pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i)) pyplot.legend() pyplot.show()
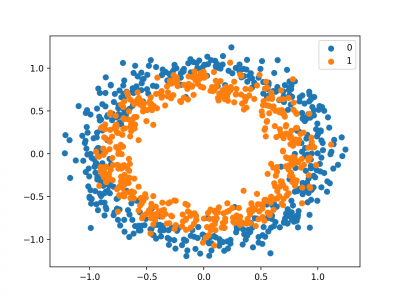
Menjalankan contoh menciptakan scatter plot contoh, di mana variabel input menentukan lokasi titik dan nilai kelas mendefinisikan warna, dengan kelas 0 biru dan oranye kelas 1.
Poin sudah diskalakan dengan cukup sekitar 0, hampir di [-1,1]. Kita tidak akan mengubah skala mereka dalam hal ini.
Dataset akan di split sama untuk train dan test set.
# split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:]
Model MLP sederhana dapat didefinisikan untuk mengatasi masalah ini yang mengharapkan dua input untuk dua fitur dalam dataset, lapisan tersembunyi dengan 50 node, fungsi aktivasi linear yang diperbaiki dan lapisan output yang perlu dikonfigurasi untuk pilihan fungsi loss.
# define model model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='...'))
Model ini akan cocok menggunakan stochastic gradient descent dengan tingkat pembelajaran default yang masuk akal 0,01 dan momentum 0,9.
opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
Kami akan mencocokkan model untuk 200 training epoch dan mengevaluasi kinerja model terhadap loss dan akurasi pada akhir setiap epoch sehingga kami dapat mem-plot kurva pembelajaran.
# fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
Sekarang kita memiliki dasar masalah dan model, kita dapat melihat mengevaluasi tiga fungsi loss umum yang sesuai untuk masalah pemodelan prediktif klasifikasi biner.
Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk klasifikasi biner.
Binary Cross-Entropy Loss
Cross-entropy adalah fungsi loss default yang digunakan untuk masalah klasifikasi biner.
Ini dimaksudkan untuk digunakan dengan klasifikasi biner di mana nilai target berada di set {0, 1}.
Secara matematis, ini adalah fungsi loss yang lebih disukai di bawah inference framework of maximum likelihood. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang bagus.
Cross-entropy akan menghitung skor yang merangkum perbedaan rata-rata antara distribusi probabilitas aktual dan prediksi untuk kelas prediksi 1. Skor tersebut diminimalkan dan nilai cross-entropy yang baik adalah 0.
Cross-entropy dapat ditentukan sebagai fungsi loss di Keras dengan menetapkan ‘binary_crossentropy‘ saat menyusun model.
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan satu simpul dan aktivasi ‘sigmoid in untuk memprediksi probabilitas untuk kelas 1.
model.add(Dense(1, activation='sigmoid'))
Contoh lengkap dari MLP dengan kehilangan lintas-entropi untuk masalah klasifikasi biner dua lingkaran tercantum di bawah ini.
# mlp for the circles problem with cross entropy loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()
Menjalankan contoh untuk mem-print akurasi klasifikasi untuk model pada dataset train dan test.
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
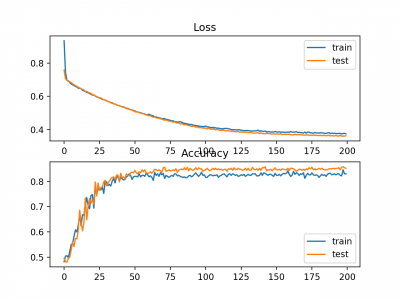
In this case, we can see that the model learned the problem reasonably well, achieving about 83% accuracy on the training dataset and about 85% on the test dataset. The scores are reasonably close, suggesting the model is probably not over or underfit.
Train: 0.836, Test: 0.852
A figure is also created showing two line plots, the top with the cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
The plot shows that the training process converged well. The plot for loss is smooth, given the continuous nature of the error between the probability distributions, whereas the line plot for accuracy shows bumps, given examples in the train and test set can ultimately only be predicted as correct or incorrect, providing less granular feedback on performance.
Hinge Loss
An alternative to cross-entropy for binary classification problems is the hinge loss function, primarily developed for use with Support Vector Machine (SVM) models.
It is intended for use with binary classification where the target values are in the set {-1, 1}.
The hinge loss function encourages examples to have the correct sign, assigning more error when there is a difference in the sign between the actual and predicted class values.
Reports of performance with the hinge loss are mixed, sometimes resulting in better performance than cross-entropy on binary classification problems.
Firstly, the target variable must be modified to have values in the set {-1, 1}.
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
The hinge loss function can then be specified as the ‘hinge‘ in the compile function.
model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
Finally, the output layer of the network must be configured to have a single node with a hyperbolic tangent activation function capable of outputting a single value in the range [-1, 1].
model.add(Dense(1, activation='tanh'))
The complete example of an MLP with a hinge loss function for the two circles binary classification problem is listed below.
# mlp for the circles problem with hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()
Running the example first prints the classification accuracy for the model on the train and test dataset.
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
In this case, we can see slightly worse performance than using cross-entropy, with the chosen model configuration with less than 80% accuracy on the train and test sets.
Train: 0.792, Test: 0.740
A figure is also created showing two line plots, the top with the hinge loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
The plot of hinge loss shows that the model has converged and has reasonable loss on both datasets. The plot of classification accuracy also shows signs of convergence, albeit at a lower level of skill than may be desirable on this problem. Line Plots of Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
Line Plots of Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
Squared Hinge Loss
The hinge loss function has many extensions, often the subject of investigation with SVM models.
A popular extension is called the squared hinge loss that simply calculates the square of the score hinge loss. It has the effect of smoothing the surface of the error function and making it numerically easier to work with.
If using a hinge loss does result in better performance on a given binary classification problem, is likely that a squared hinge loss may be appropriate.
As with using the hinge loss function, the target variable must be modified to have values in the set {-1, 1}.
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
The squared hinge loss can be specified as ‘squared_hinge‘ in the compile() function when defining the model.
model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
And finally, the output layer must use a single node with a hyperbolic tangent activation function capable of outputting continuous values in the range [-1, 1].
model.add(Dense(1, activation='tanh'))
The complete example of an MLP with the squared hinge loss function on the two circles binary classification problem is listed below.
# mlp for the circles problem with squared hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()
Running the example first prints the classification accuracy for the model on the train and test datasets.
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
In this case, we can see that for this problem and the chosen model configuration, the hinge squared loss may not be appropriate, resulting in classification accuracy of less than 70% on the train and test sets.
Train: 0.682, Test: 0.646
A figure is also created showing two line plots, the top with the squared hinge loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
The plot of loss shows that indeed, the model converged, but the shape of the error surface is not as smooth as other loss functions where small changes to the weights are causing large changes in loss. Line Plots of Squared Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
Line Plots of Squared Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
Multi-Class Classification Loss Functions
Multi-Class classification are those predictive modeling problems where examples are assigned one of more than two classes.
The problem is often framed as predicting an integer value, where each class is assigned a unique integer value from 0 to (num_classes – 1). The problem is often implemented as predicting the probability of the example belonging to each known class.
In this section, we will investigate loss functions that are appropriate for multi-class classification predictive modeling problems.
We will use the blobs problem as the basis for the investigation. The make_blobs() function provided by the scikit-learn provides a way to generate examples given a specified number of classes and input features. We will use this function to generate 1,000 examples for a 3-class classification problem with 2 input variables. The pseudorandom number generator will be seeded consistently so that the same 1,000 examples are generated each time the code is run.
# generate dataset X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
The two input variables can be taken as x and y coordinates for points on a two-dimensional plane.
The example below creates a scatter plot of the entire dataset coloring points by their class membership.
# scatter plot of blobs dataset from sklearn.datasets.samples_generator import make_blobs from numpy import where from matplotlib import pyplot # generate dataset X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # select indices of points with each class label for i in range(3): samples_ix = where(y == i) pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1]) pyplot.show()
Running the example creates a scatter plot showing the 1,000 examples in the dataset with examples belonging to the 0, 1, and 2 classes colors blue, orange, and green respectively. Scatter Plot of Examples Generated from the Blobs Multi-Class Classification Problem
Scatter Plot of Examples Generated from the Blobs Multi-Class Classification Problem
The input features are Gaussian and could benefit from standardization; nevertheless, we will keep the values unscaled in this example for brevity.
The dataset will be split evenly between train and test sets.
# split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:]
A small MLP model will be used as the basis for exploring loss functions.
The model expects two input variables, has 50 nodes in the hidden layer and the rectified linear activation function, and an output layer that must be customized based on the selection of the loss function.
# define model model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(..., activation='...'))
The model is fit using stochastic gradient descent with a sensible default learning rate of 0.01 and a momentum of 0.9.
# compile model opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
The model will be fit for 100 epochs on the training dataset and the test dataset will be used as a validation dataset, allowing us to evaluate both loss and classification accuracy on the train and test sets at the end of each training epoch and draw learning curves.
# fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
Now that we have the basis of a problem and model, we can take a look evaluating three common loss functions that are appropriate for a multi-class classification predictive modeling problem.
Although an MLP is used in these examples, the same loss functions can be used when training CNN and RNN models for multi-class classification.
Multi-Class Cross-Entropy Loss
Cross-entropy is the default loss function to use for multi-class classification problems.
In this case, it is intended for use with multi-class classification where the target values are in the set {0, 1, 3, …, n}, where each class is assigned a unique integer value.
Mathematically, it is the preferred loss function under the inference framework of maximum likelihood. It is the loss function to be evaluated first and only changed if you have a good reason.
Cross-entropy will calculate a score that summarizes the average difference between the actual and predicted probability distributions for all classes in the problem. The score is minimized and a perfect cross-entropy value is 0.
Cross-entropy can be specified as the loss function in Keras by specifying ‘categorical_crossentropy‘ when compiling the model.
The function requires that the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.
model.add(Dense(3, activation='softmax'))
In turn, this means that the target variable must be one hot encoded.
This is to ensure that each example has an expected probability of 1.0 for the actual class value and an expected probability of 0.0 for all other class values. This can be achieved using the to_categorical() Keras function.
# one hot encode output variable y = to_categorical(y)
The complete example of an MLP with cross-entropy loss for the multi-class blobs classification problem is listed below.
# mlp for the blobs multi-class classification problem with cross-entropy loss
from sklearn.datasets.samples_generator import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
Running the example first prints the classification accuracy for the model on the train and test dataset.
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
In this case, we can see the model performed well, achieving a classification accuracy of about 84% on the training dataset and about 82% on the test dataset.
Train: 0.840, Test: 0.822
A figure is also created showing two line plots, the top with the cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
In this case, the plot shows the model seems to have converged. The line plots for both cross-entropy and accuracy both show good convergence behavior, although somewhat bumpy. The model may be well configured given no sign of over or under fitting. The learning rate or batch size may be tuned to even out the smoothness of the convergence in this case. Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
Sparse Multiclass Cross-Entropy Loss
A possible cause of frustration when using cross-entropy with classification problems with a large number of labels is the one hot encoding process.
For example, predicting words in a vocabulary may have tens or hundreds of thousands of categories, one for each label. This can mean that the target element of each training example may require a one hot encoded vector with tens or hundreds of thousands of zero values, requiring significant memory.
Sparse cross-entropy addresses this by performing the same cross-entropy calculation of error, without requiring that the target variable be one hot encoded prior to training.
Sparse cross-entropy can be used in keras for multi-class classification by using ‘sparse_categorical_crossentropy‘ when calling the compile() function.
model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
The function requires that the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.
model.add(Dense(3, activation='softmax'))
No one hot encoding of the target variable is required, a benefit of this loss function.
The complete example of training an MLP with sparse cross-entropy on the blobs multi-class classification problem is listed below.
# mlp for the blobs multi-class classification problem with sparse cross-entropy loss
from sklearn.datasets.samples_generator import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()
Running the example first prints the classification accuracy for the model on the train and test dataset.
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
In this case, we can see the model achieves good performance on the problem. In fact, if you repeat the experiment many times, the average performance of sparse and non-sparse cross-entropy should be comparable.
Train: 0.832, Test: 0.818
A figure is also created showing two line plots, the top with the sparse cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
In this case, the plot shows good convergence of the model over training with regard to loss and classification accuracy. Line Plots of Sparse Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
Line Plots of Sparse Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
Kullback Leibler Divergence Loss
Kullback Leibler Divergence, or KL Divergence for short, is a measure of how one probability distribution differs from a baseline distribution.
A KL divergence loss of 0 suggests the distributions are identical. In practice, the behavior of KL Divergence is very similar to cross-entropy. It calculates how much information is lost (in terms of bits) if the predicted probability distribution is used to approximate the desired target probability distribution.
As such, the KL divergence loss function is more commonly used when using models that learn to approximate a more complex function than simply multi-class classification, such as in the case of an autoencoder used for learning a dense feature representation under a model that must reconstruct the original input. In this case, KL divergence loss would be preferred. Nevertheless, it can be used for multi-class classification, in which case it is functionally equivalent to multi-class cross-entropy.
KL divergence loss can be used in Keras by specifying ‘kullback_leibler_divergence‘ in the compile() function.
model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])
As with cross-entropy, the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.
Also, as with categorical cross-entropy, we must one hot encode the target variable to have an expected probability of 1.0 for the class value and 0.0 for all other class values.
# one hot encode output variable y = to_categorical(y)
The complete example of training an MLP with KL divergence loss for the blobs multi-class classification problem is listed below.
# mlp for the blobs multi-class classification problem with kl divergence loss
from sklearn.datasets.samples_generator import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()
Running the example first prints the classification accuracy for the model on the train and test dataset.
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
In this case, we see performance that is similar to those results seen with cross-entropy loss, in this case about 82% accuracy on the train and test dataset.
Train: 0.822, Test: 0.822
A figure is also created showing two line plots, the top with the KL divergence loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
In this case, the plot shows good convergence behavior for both loss and classification accuracy. It is very likely that an evaluation of cross-entropy would result in nearly identical behavior given the similarities in the measure. Line Plots of KL Divergence Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
Line Plots of KL Divergence Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Posts
- Loss and Loss Functions for Training Deep Learning Neural Networks
Papers
- On Loss Functions for Deep Neural Networks in Classification, 2017.
Referensi