Difference between revisions of "Keras: Memilih Fungsi Loss"

From OnnoWiki
Jump to navigation Jump to search
 
(39 intermediate revisions by the same user not shown)
Line 137: Line 137:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the mean squared error for the model on the train and test datasets.
+
Menjalankan contoh pertama mem-print kesalahan kuadrat rata-rata model pada train dan test dataset.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, Basil spesifik dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see that the model learned the problem achieving zero error, at least to three decimal places.
+
Dalam kasus ini, kita dapat melihat bahwa model berusaha mencapai nol kesalahan, setidaknya sampai tiga tempat desimal.
  
 
  Train: 0.000, Test: 0.001
 
  Train: 0.000, Test: 0.001
  
−
A line plot is also created showing the mean squared error loss over the training epochs for both the train (blue) and test (orange) sets.
+
Plot garis juga dibuat menunjukkan mean squared error loss selama periode pelatihan untuk set train (biru) dan test (oranye).
  
−
We can see that the model converged reasonably quickly and both train and test performance remained equivalent. The performance and convergence behavior of the model suggest that mean squared error is a good match for a neural network learning this problem.
+
Kita dapat melihat bahwa model terkonvergensi dengan cukup cepat dan baik kinerja train dan test tetap setara. Perilaku kinerja dan konvergensi model menunjukkan bahwa mean squared error cocok untuk neural network yang mempelajari masalah ini.
  
 
[[File:Line-plot-of-Mean-Squared-Error-Loss-over-Training-Epochs-When-Optimizing-the-Mean-Squared-Error-Loss-Function.png|center|400px|thumb]]
 
[[File:Line-plot-of-Mean-Squared-Error-Loss-over-Training-Epochs-When-Optimizing-the-Mean-Squared-Error-Loss-Function.png|center|400px|thumb]]
Line 153: Line 153:
 
===Mean Squared Logarithmic Error Loss===
 
===Mean Squared Logarithmic Error Loss===
  
−
There may be regression problems in which the target value has a spread of values and when predicting a large value, you may not want to punish a model as heavily as mean squared error.
+
Mungkin ada masalah regresi di mana nilai target memiliki penyebaran nilai dan ketika memprediksi nilai besar, kita mungkin tidak ingin menghukum model sebanyak kesalahan kuadrat rata-rata.
  
−
Instead, you can first calculate the natural logarithm of each of the predicted values, then calculate the mean squared error. This is called the Mean Squared Logarithmic Error loss, or MSLE for short.
+
Sebagai gantinya, kita pertama-tama dapat menghitung nilai log dari masing-masing nilai yang diprediksi, lalu menghitung rata-rata kesalahan kuadrat. Ini disebut Mean Squared Logarithmic Error loss, atau disingkat MSLE.
  
−
It has the effect of relaxing the punishing effect of large differences in large predicted values.
+
Ini memiliki efek membuat santai efek punishing saat ada perbedaan besar dalam nilai prediksi yang besar.
  
−
As a loss measure, it may be more appropriate when the model is predicting unscaled quantities directly. Nevertheless, we can demonstrate this loss function using our simple regression problem.
+
Sebagai ukuran loss, mungkin lebih tepat ketika model memprediksi unscaled quantities secara langsung. Namun demikian, kita dapat menunjukkan fungsi loss ini menggunakan masalah regresi sederhana.
  
−
The model can be updated to use the ‘mean_squared_logarithmic_error‘ loss function and keep the same configuration for the output layer. We will also track the mean squared error as a metric when fitting the model so that we can use it as a measure of performance and plot the learning curve.
+
Model ini dapat diperbarui untuk menggunakan fungsi loss ‘mean_squared_logarithmic_error‘ dan mempertahankan konfigurasi yang sama untuk layer output. Kita juga akan melacak mean squared error sebagai metrik saat memasang model sehingga kita dapat menggunakannya sebagai ukuran kinerja dan plot kurva pembelajaran.
  
 
  model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
 
  model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
  
−
The complete example of using the MSLE loss function is listed below.
+
Contoh lengkap menggunakan fungsi loss MSLE tercantum di bawah ini.
  
 
  # mlp for regression with msle loss function
 
  # mlp for regression with msle loss function
Line 209: Line 209:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the mean squared error for the model on the train and test dataset.
+
Menjalankan contoh pertama mem-print  mean squared error untuk model pada  datset train dan test.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh tersebut beberapa kali.
  
−
In this case, we can see that the model resulted in slightly worse MSE on both the training and test dataset. It may not be a good fit for this problem as the distribution of the target variable is a standard Gaussian.
+
Dalam hal ini, kita dapat melihat bahwa model tersebut menghasilkan MSE yang sedikit lebih buruk pada datset training dan testing. Ini mungkin tidak cocok untuk masalah ini karena distribusi variabel target adalah standar Gaussian.
  
 
  Train: 0.165, Test: 0.184
 
  Train: 0.165, Test: 0.184
  
−
A line plot is also created showing the mean squared logarithmic error loss over the training epochs for both the train (blue) and test (orange) sets (top), and a similar plot for the mean squared error (bottom).
+
Plot garis juga dibuat menunjukkan mean squared logarithmic error losst selama periode training untuk set train (biru) dan test (oranye) (atas), dan plot yang sama untuk mean squared error (bawah).
  
−
We can see that the MSLE converged well over the 100 epochs algorithm; it appears that the MSE may be showing signs of overfitting the problem, dropping fast and starting to rise from epoch 20 onwards.
+
Kita dapat melihat bahwa algoritma MSLE konvergen lebih dari a100 epoch; tampaknya MSE mungkin menunjukkan tanda-tanda overfitting dari masalah yang ada, jatuh secara cepat cepat dan mulai naik pada epoch 20 dan seterusnya.
  
  
Line 227: Line 227:
 
===Mean Absolute Error Loss===
 
===Mean Absolute Error Loss===
  
−
On some regression problems, the distribution of the target variable may be mostly Gaussian, but may have outliers, e.g. large or small values far from the mean value.
+
Pada beberapa masalah regresi, distribusi variabel target mungkin sebagian besar Gaussian, tetapi mungkin memiliki outlier, mis. nilai besar atau kecil jauh dari nilai rata-rata.
  
−
The Mean Absolute Error, or MAE, loss is an appropriate loss function in this case as it is more robust to outliers. It is calculated as the average of the absolute difference between the actual and predicted values.
+
The Mean Absolute Error loss, atau MAE, adalah fungsi loss yang sesuai dalam kasus ini karena itu lebih kuat untuk outlier. Ini dihitung sebagai rata-rata perbedaan absolut antara nilai aktual dan prediksi.
  
−
The model can be updated to use the ‘mean_absolute_error‘ loss function and keep the same configuration for the output layer.
+
Model dapat diperbarui untuk menggunakan fungsi loss ‘mean_absolute_error‘ dan mempertahankan konfigurasi yang sama untuk layer output.
  
 
  model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
 
  model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
  
−
The complete example using the mean absolute error as the loss function on the regression test problem is listed below.
+
Contoh lengkap menggunakan  mean absolute error sebagai fungsi loss pada masalah test regresi terlampir di bawah ini.
  
 
  # mlp for regression with mae loss function
 
  # mlp for regression with mae loss function
Line 279: Line 279:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the mean squared error for the model on the train and test dataset.
+
Menjalankan contoh pertama mem-print mean squared error untuk model dataset train dan test.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see that the model learned the problem, achieving a near zero error, at least to three decimal places.
+
Dalam kasus ini, kita dapat melihat bahwa model learn masalah, mencapai kesalahan mendekati nol, setidaknya ke tiga tempat desimal.
  
 
  Train: 0.002, Test: 0.002
 
  Train: 0.002, Test: 0.002
  
−
A line plot is also created showing the mean absolute error loss over the training epochs for both the train (blue) and test (orange) sets (top), and a similar plot for the mean squared error (bottom).
+
Plot garis juga dibuat yang menunjukkan mean absolute error loss selama periode pelatihan untuk set train (biru) dan test (oranye) (atas), dan plot serupa untuk mean squared error (bawah).
  
−
In this case, we can see that MAE does converge but shows a bumpy course, although the dynamics of MSE don’t appear greatly affected. We know that the target variable is a standard Gaussian with no large outliers, so MAE would not be a good fit in this case.
+
Dalam hal ini, kita dapat melihat bahwa MAE memang konvergen akan tetapi pencapaiannya bergelombang, meskipun dinamika MSE tidak tampak sangat terpengaruh. Kita tahu bahwa variabel target adalah Gaussian standar tanpa outlier besar, sehingga MAE tidak cocok untuk kasus ini.
−
 
 
−
It might be more appropriate on this problem if we did not scale the target variable first.
 
  
 +
Mungkin lebih tepat untuk masalah ini jika kita tidak menskalakan variabel target terlebih dahulu.
  
 
[[File:Line-plots-of-Mean-Absolute-Error-Loss-and-Mean-Squared-Error-over-Training-Epochs.png|center|400px|thumb]]
 
[[File:Line-plots-of-Mean-Absolute-Error-Loss-and-Mean-Squared-Error-over-Training-Epochs.png|center|400px|thumb]]
  
−
==Binary Classification Loss Functions==
+
==Binary Classification Loss Function==
  
−
Binary classification are those predictive modeling problems where examples are assigned one of two labels.
+
Klasifikasi biner adalah masalah-masalah pemodelan prediktif di mana contoh diberikan satu dari dua label.
  
−
The problem is often framed as predicting a value of 0 or 1 for the first or second class and is often implemented as predicting the probability of the example belonging to class value 1.
+
Masalahnya sering di lihat sebagai memprediksi nilai 0 atau 1 untuk kelas pertama atau kedua dan sering diimplementasikan sebagai memprediksi probabilitas milik nilai kelas 1.
  
−
In this section, we will investigate loss functions that are appropriate for binary classification predictive modeling problems.
+
Pada bagian ini, kami akan menyelidiki fungsi kerugian yang sesuai untuk masalah pemodelan prediktif klasifikasi biner.
  
−
We will generate examples from the circles test problem in scikit-learn as the basis for this investigation. The circles problem involves samples drawn from two concentric circles on a two-dimensional plane, where points on the outer circle belong to class 0 and points for the inner circle belong to class 1. Statistical noise is added to the samples to add ambiguity and make the problem more challenging to learn.
+
Kami akan menghasilkan contoh dari masalah test lingkaran di scikit-belajar sebagai basis untuk penelitian ini. Masalah lingkaran melibatkan sampel yang diambil dari dua lingkaran konsentris pada bidang dua dimensi, di mana titik pada lingkaran luar milik kelas 0 dan titik untuk lingkaran dalam milik kelas 1. Noise statistik ditambahkan ke sampel untuk menambah ambiguitas dan membuat masalahnya lebih sulit untuk dipelajari.
  
−
We will generate 1,000 examples and add 10% statistical noise. The pseudorandom number generator will be seeded with the same value to ensure that we always get the same 1,000 examples.
+
Kami akan men-generate 1.000 contoh dan menambahkan 10% noise statistik. Generator nomor pseudorandom akan di-seed dengan nilai yang sama untuk memastikan bahwa kami selalu mendapatkan 1.000 contoh yang sama.
  
 
  # generate circles
 
  # generate circles
 
  X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
 
  X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
  
−
We can create a scatter plot of the dataset to get an idea of the problem we are modeling. The complete example is listed below.
+
Kita dapat membuat scatter plot dataset untuk mendapatkan gambaran tentang masalah yang kita modelkan. Contoh lengkapnya tercantum di bawah ini.
  
 
  # scatter plot of the circles dataset with points colored by class
 
  # scatter plot of the circles dataset with points colored by class
Line 326: Line 325:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example creates a scatter plot of the examples, where the input variables define the location of the point and the class value defines the color, with class 0 blue and class 1 orange.
+
Menjalankan contoh menciptakan scatter plot contoh, di mana variabel input menentukan lokasi titik dan nilai kelas mendefinisikan warna, dengan kelas 0 biru dan oranye kelas 1.
−
Scatter Plot of Dataset for the Circles Binary Classification Problem
 
  
−
Scatter Plot of Dataset for the Circles Binary Classification Problem
+
[[File:Scatter-Plot-of-Dataset-for-the-Circles-Binary-Classification-Problem.png|center|400px|thumb]]
  
−
The points are already reasonably scaled around 0, almost in [-1,1]. We won’t rescale them in this case.
+
Poin sudah diskalakan dengan cukup sekitar 0, hampir di [-1,1]. Kita tidak akan mengubah skala mereka dalam hal ini.
  
−
The dataset is split evenly for train and test sets.
+
Dataset akan di split sama untuk train dan test set.
  
 
  # split into train and test
 
  # split into train and test
Line 340: Line 338:
 
  trainy, testy = y[:n_train], y[n_train:]
 
  trainy, testy = y[:n_train], y[n_train:]
  
−
A simple MLP model can be defined to address this problem that expects two inputs for the two features in the dataset, a hidden layer with 50 nodes, a rectified linear activation function and an output layer that will need to be configured for the choice of loss function.
+
Model MLP sederhana dapat didefinisikan untuk mengatasi masalah ini yang mengharapkan dua input untuk dua fitur dalam dataset, lapisan tersembunyi dengan 50 node, fungsi aktivasi linear yang diperbaiki dan lapisan output yang perlu dikonfigurasi untuk pilihan fungsi loss.
  
 
  # define model
 
  # define model
Line 347: Line 345:
 
  model.add(Dense(1, activation='...'))
 
  model.add(Dense(1, activation='...'))
  
−
The model will be fit using stochastic gradient descent with the sensible default learning rate of 0.01 and momentum of 0.9.
+
Model ini akan cocok menggunakan stochastic gradient descent dengan tingkat pembelajaran default yang masuk akal 0,01 dan momentum 0,9.
  
 
  opt = SGD(lr=0.01, momentum=0.9)
 
  opt = SGD(lr=0.01, momentum=0.9)
 
  model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
  
−
We will fit the model for 200 training epochs and evaluate the performance of the model against the loss and accuracy at the end of each epoch so that we can plot learning curves.
+
Kami akan mencocokkan model untuk 200 training epoch dan mengevaluasi kinerja model terhadap loss dan akurasi pada akhir setiap epoch sehingga kami dapat mem-plot kurva pembelajaran.
  
 
  # fit model
 
  # fit model
 
  history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
 
  history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
  
−
Now that we have the basis of a problem and model, we can take a look evaluating three common loss functions that are appropriate for a binary classification predictive modeling problem.
+
Sekarang kita memiliki dasar masalah dan model, kita dapat melihat mengevaluasi tiga fungsi loss umum yang sesuai untuk masalah pemodelan prediktif klasifikasi biner.
  
−
Although an MLP is used in these examples, the same loss functions can be used when training CNN and RNN models for binary classification.
+
Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk klasifikasi biner.
  
 
===Binary Cross-Entropy Loss===
 
===Binary Cross-Entropy Loss===
  
−
Cross-entropy is the default loss function to use for binary classification problems.
+
Cross-entropy adalah fungsi loss default yang digunakan untuk masalah klasifikasi biner.
  
−
It is intended for use with binary classification where the target values are in the set {0, 1}.
+
Ini dimaksudkan untuk digunakan dengan klasifikasi biner di mana nilai target berada di set {0, 1}.
  
−
Mathematically, it is the preferred loss function under the inference framework of maximum likelihood. It is the loss function to be evaluated first and only changed if you have a good reason.
+
Secara matematis, ini adalah fungsi loss yang lebih disukai di bawah inference framework of maximum likelihood. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang bagus.
  
−
Cross-entropy will calculate a score that summarizes the average difference between the actual and predicted probability distributions for predicting class 1. The score is minimized and a perfect cross-entropy value is 0.
+
Cross-entropy akan menghitung skor yang merangkum perbedaan rata-rata antara distribusi probabilitas aktual dan prediksi untuk kelas prediksi 1. Skor tersebut diminimalkan dan nilai cross-entropy yang baik adalah 0.
  
−
Cross-entropy can be specified as the loss function in Keras by specifying ‘binary_crossentropy‘ when compiling the model.
+
Cross-entropy dapat ditentukan sebagai fungsi loss di Keras dengan menetapkan ‘binary_crossentropy‘ saat menyusun model.
  
 
  model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
  
−
The function requires that the output layer is configured with a single node and a ‘sigmoid‘ activation in order to predict the probability for class 1.
+
Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan satu simpul dan aktivasi ‘sigmoid in untuk memprediksi probabilitas untuk kelas 1.
  
 
  model.add(Dense(1, activation='sigmoid'))
 
  model.add(Dense(1, activation='sigmoid'))
  
−
The complete example of an MLP with cross-entropy loss for the two circles binary classification problem is listed below.
+
Contoh lengkap dari MLP dengan kehilangan lintas-entropi untuk masalah klasifikasi biner dua lingkaran tercantum di bawah ini.
  
 
  # mlp for the circles problem with cross entropy loss
 
  # mlp for the circles problem with cross entropy loss
Line 419: Line 417:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the classification accuracy for the model on the train and test dataset.
+
Menjalankan contoh untuk mem-print akurasi klasifikasi untuk model pada dataset train dan test.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see that the model learned the problem reasonably well, achieving about 83% accuracy on the training dataset and about 85% on the test dataset. The scores are reasonably close, suggesting the model is probably not over or underfit.
+
Dalam hal ini, kita dapat melihat bahwa model bisa learn masalah dengan cukup baik, mencapai akurasi sekitar 83% pada dataset train dan sekitar 85% pada dataset test. Skor cukup dekat, menunjukkan bahwa model yang di peroleh mungkin tidak over atau underfit.
  
 
  Train: 0.836, Test: 0.852
 
  Train: 0.836, Test: 0.852
  
−
A figure is also created showing two line plots, the top with the cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
+
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan cross-entropy loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan classification accuracy over epochs.
  
−
The plot shows that the training process converged well. The plot for loss is smooth, given the continuous nature of the error between the probability distributions, whereas the line plot for accuracy shows bumps, given examples in the train and test set can ultimately only be predicted as correct or incorrect, providing less granular feedback on performance.
+
Plot menunjukkan bahwa proses trainig konvergsi dengan baik. Plot untuk loss baik, mengingat sifat kesalahan yang kontinyu antara distribusi probabilitas, sedangkan plot garis untuk akurasi menunjukkan adanya tonjolan, memberikan contoh dataset train dan test pada akhirnya hanya dapat diprediksi sebagai benar atau salah, memberikan umpan balik yang kurang terperinci pada kinerja.
−
Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
 
  
−
Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
+
[[File:Line-Plots-of-Cross-Entropy-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Two-Circles-Binary-Classification-Problem.png|center|400px|thumb]]
  
 
===Hinge Loss===
 
===Hinge Loss===
  
−
An alternative to cross-entropy for binary classification problems is the hinge loss function, primarily developed for use with Support Vector Machine (SVM) models.
+
Alternatif untuk cross-entropy untuk masalah klasifikasi biner adalah fungsi hinge loss, terutama dikembangkan untuk digunakan dengan model Support Vector Machine (SVM).
  
−
It is intended for use with binary classification where the target values are in the set {-1, 1}.
+
Ini dimaksudkan untuk digunakan dengan klasifikasi biner di mana nilai target berada di set {-1, 1}.
  
−
The hinge loss function encourages examples to have the correct sign, assigning more error when there is a difference in the sign between the actual and predicted class values.
+
Fungsi kehilangan engsel mendorong contoh untuk memiliki tanda yang benar, menetapkan lebih banyak kesalahan ketika ada perbedaan dalam tanda antara nilai kelas aktual dan prediksi.
  
−
Reports of performance with the hinge loss are mixed, sometimes resulting in better performance than cross-entropy on binary classification problems.
+
Laporan kinerja dengan hinge loss beragam, kadang-kadang menghasilkan kinerja yang lebih baik daripada  cross-entropy pada masalah klasifikasi biner.
  
−
Firstly, the target variable must be modified to have values in the set {-1, 1}.
+
Pertama, variabel target harus dimodifikasi untuk memiliki nilai dalam set {-1, 1}.
  
 
  # change y from {0,1} to {-1,1}
 
  # change y from {0,1} to {-1,1}
 
  y[where(y == 0)] = -1
 
  y[where(y == 0)] = -1
  
−
The hinge loss function can then be specified as the ‘hinge‘ in the compile function.
+
Fungsi hinge loss dapat diset ‘hinge‘ dalam fungsi compile.
  
 
  model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
  
−
Finally, the output layer of the network must be configured to have a single node with a hyperbolic tangent activation function capable of outputting a single value in the range [-1, 1].
+
Akhirnya, lapisan output dari jaringan harus dikonfigurasi untuk memiliki satu simpul dengan fungsi aktivasi hyperbolic tangent yang mampu menghasilkan nilai tunggal dalam kisaran [-1, 1].
  
 
  model.add(Dense(1, activation='tanh'))
 
  model.add(Dense(1, activation='tanh'))
  
−
The complete example of an MLP with a hinge loss function for the two circles binary classification problem is listed below.
+
Contoh lengkap MLP dengan fungsi hinge loss untuk two circles binary classification problem tercantum di bawah ini.
  
 
  # mlp for the circles problem with hinge loss
 
  # mlp for the circles problem with hinge loss
Line 500: Line 497:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the classification accuracy for the model on the train and test dataset.
+
Menjalankan contoh pertama-tama mem-print classification accuracy untuk model pada dataset train dan test.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see slightly worse performance than using cross-entropy, with the chosen model configuration with less than 80% accuracy on the train and test sets.
+
Dalam hal ini, kita dapat melihat kinerja yang sedikit lebih buruk daripada menggunakan cross-entropy, dengan konfigurasi model yang dipilih dengan akurasi kurang dari 80% pada dataset train dan test.
  
 
  Train: 0.792, Test: 0.740
 
  Train: 0.792, Test: 0.740
Line 510: Line 507:
 
A figure is also created showing two line plots, the top with the hinge loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
 
A figure is also created showing two line plots, the top with the hinge loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
  
−
The plot of hinge loss shows that the model has converged and has reasonable loss on both datasets. The plot of classification accuracy also shows signs of convergence, albeit at a lower level of skill than may be desirable on this problem.
+
Plot hinge loss menunjukkan bahwa model telah konvergen dan memiliki loss yang wajar pada kedua dataset. Alur akurasi klasifikasi juga menunjukkan tanda-tanda konvergensi, meskipun pada tingkat kinerja yang lebih rendah daripada yang diinginkan pada masalah ini.
−
Line Plots of Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
+
 
  
−
Line Plots of Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
+
[[File:Line-Plots-of-Hinge-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Two-Circles-Binary-Classification-Problem.png|center|400px|thumb]]
  
 
===Squared Hinge Loss===
 
===Squared Hinge Loss===
  
−
The hinge loss function has many extensions, often the subject of investigation with SVM models.
+
Fungsi hinge loss memiliki banyak pengembangan, seringkali menjadi subjek investigasi dengan model SVM.
  
−
A popular extension is called the squared hinge loss that simply calculates the square of the score hinge loss. It has the effect of smoothing the surface of the error function and making it numerically easier to work with.
+
Pengembangan yang populer disebut squared hinge loss yang hanya menghitung kuadrat dari score hinge loss. Ini memiliki efek menghaluskan permukaan fungsi kesalahan dan membuatnya lebih mudah untuk dikerjakan secara numerik.
  
−
If using a hinge loss does result in better performance on a given binary classification problem, is likely that a squared hinge loss may be appropriate.
+
Jika menggunakan hinge loss memang menghasilkan kinerja yang lebih baik pada masalah klasifikasi biner yang diberikan, kemungkinan bahwa squared hinge loss mungkin sesuai.
  
−
As with using the hinge loss function, the target variable must be modified to have values in the set {-1, 1}.
+
Seperti halnya menggunakan fungsi hinge loss, variabel target harus dimodifikasi untuk memiliki nilai dalam set {-1, 1}.
  
 
  # change y from {0,1} to {-1,1}
 
  # change y from {0,1} to {-1,1}
 
  y[where(y == 0)] = -1
 
  y[where(y == 0)] = -1
  
−
The squared hinge loss can be specified as ‘squared_hinge‘ in the compile() function when defining the model.
+
Squared hinge loss dapat ditentukan sebagai ‘squared_hinge‘ dalam fungsi compile() saat mendefinisikan model.
  
 
  model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
  
−
And finally, the output layer must use a single node with a hyperbolic tangent activation function capable of outputting continuous values in the range [-1, 1].
+
Dan akhirnya, lapisan output harus menggunakan node tunggal dengan fungsi aktivasi tangen hiperbolik yang mampu menghasilkan nilai kontinu dalam kisaran [-1, 1].
  
 
  model.add(Dense(1, activation='tanh'))
 
  model.add(Dense(1, activation='tanh'))
  
−
The complete example of an MLP with the squared hinge loss function on the two circles binary classification problem is listed below.
+
Contoh lengkap dari MLP dengan fungsi squared hinge loss pada masalah klasifikasi biner dua lingkaran tercantum di bawah ini.
  
 
  # mlp for the circles problem with squared hinge loss
 
  # mlp for the circles problem with squared hinge loss
Line 579: Line 576:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the classification accuracy for the model on the train and test datasets.
+
Menjalankan contoh pertama-tama memprint keakuratan klasifikasi untuk model pada dataset train dan test.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma pelatihan, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see that for this problem and the chosen model configuration, the hinge squared loss may not be appropriate, resulting in classification accuracy of less than 70% on the train and test sets.
+
Dalam kasus ini, kita dapat melihat bahwa untuk masalah ini dan konfigurasi model yang dipilih, hinge squared loss mungkin tidak sesuai, sehingga akurasi klasifikasi kurang dari 70% pada dataset train dan test.
  
 
  Train: 0.682, Test: 0.646
 
  Train: 0.682, Test: 0.646
  
−
A figure is also created showing two line plots, the top with the squared hinge loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
+
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan squared hinge loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan classification accuracy over epochs.
  
−
The plot of loss shows that indeed, the model converged, but the shape of the error surface is not as smooth as other loss functions where small changes to the weights are causing large changes in loss.
+
Plot loss menunjukkan bahwa memang, model konvergensi, tetapi bentuk permukaan error tidak semulus fungsi loss lainnya di mana perubahan kecil pada nilai weight menyebabkan perubahan besar loss.
−
Line Plots of Squared Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
 
  
−
Line Plots of Squared Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem
+
[[File:Line-Plots-of-Squared-Hinge-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Two-Circles-Binary-Classification-Problem.png|center|400px|thumb]]
  
 
==Multi-Class Classification Loss Functions==
 
==Multi-Class Classification Loss Functions==
  
−
Multi-Class classification are those predictive modeling problems where examples are assigned one of more than two classes.
+
Multi-Class classification adalah masalah-masalah pemodelan prediktif di mana contoh diberikan satu dari lebih dari dua kelas.
  
−
The problem is often framed as predicting an integer value, where each class is assigned a unique integer value from 0 to (num_classes – 1). The problem is often implemented as predicting the probability of the example belonging to each known class.
+
Masalahnya sering di frame untuk memprediksi nilai integer, di mana setiap kelas diberi nilai integer unik dari 0 hingga (num_classes - 1). Masalahnya sering diimplementasikan sebagai memprediksi probabilitas dari contoh milik masing-masing kelas yang dikenal.
  
−
In this section, we will investigate loss functions that are appropriate for multi-class classification predictive modeling problems.
+
Pada bagian ini, kita akan melihat fungsi loss yang sesuai untuk multi-class classification predictive modeling problems.
  
−
We will use the blobs problem as the basis for the investigation. The make_blobs() function provided by the scikit-learn provides a way to generate examples given a specified number of classes and input features. We will use this function to generate 1,000 examples for a 3-class classification problem with 2 input variables. The pseudorandom number generator will be seeded consistently so that the same 1,000 examples are generated each time the code is run.
+
Kita akan menggunakan masalah blobs sebagai dasar untuk penelitian. Fungsi make_blobs() yang disediakan oleh scikit-learn menyediakan cara untuk men-generate contoh yang diberikan sejumlah kelas dan fitur input tertentu. Kita akan menggunakan fungsi ini untuk menghasilkan 1.000 contoh untuk masalah klasifikasi 3-kelas dengan 2 variabel input. Generator nomor pseudorandom akan di-seed secara konsisten sehingga 1.000 contoh yang sama dihasilkan setiap kali kode dijalankan.
  
 
  # generate dataset
 
  # generate dataset
 
  X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
 
  X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
  
−
The two input variables can be taken as x and y coordinates for points on a two-dimensional plane.
+
Dua variabel input dapat diambil sebagai koordinat x dan y untuk titik pada bidang dua dimensi.
  
−
The example below creates a scatter plot of the entire dataset coloring points by their class membership.
+
Contoh di bawah ini membuat sebaran plot dari seluruh titik pewarnaan dataset oleh keanggotaan kelas mereka.
  
 
  # scatter plot of blobs dataset
 
  # scatter plot of blobs dataset
Line 623: Line 619:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example creates a scatter plot showing the 1,000 examples in the dataset with examples belonging to the 0, 1, and 2 classes colors blue, orange, and green respectively.
+
Menjalankan contoh membuat scatter plot yang menunjukkan 1.000 contoh dalam dataset dengan contoh milik kelas 0, 1, dan 2 warna biru, oranye, dan hijau.
−
Scatter Plot of Examples Generated from the Blobs Multi-Class Classification Problem
 
  
−
Scatter Plot of Examples Generated from the Blobs Multi-Class Classification Problem
+
[[File:Scatter-Plot-of-Examples-Generated-from-the-Blobs-Multi-Class-Classification-Problem.png|center|400px|thumb]]
  
−
The input features are Gaussian and could benefit from standardization; nevertheless, we will keep the values unscaled in this example for brevity.
+
Fitur input Gaussian dan dapat mengambil manfaat dari standardisasi; namun demikian, kita akan menjaga nilai-nilai tetap dalam contoh ini untuk mempersingkat.
  
−
The dataset will be split evenly between train and test sets.
+
Dataset akan dibagi secara merata antara dataset training dan testing.
  
 
  # split into train and test
 
  # split into train and test
Line 637: Line 632:
 
  trainy, testy = y[:n_train], y[n_train:]
 
  trainy, testy = y[:n_train], y[n_train:]
  
−
A small MLP model will be used as the basis for exploring loss functions.
+
Model MLP kecil akan digunakan sebagai dasar untuk mengeksplorasi fungsi loss.
  
−
The model expects two input variables, has 50 nodes in the hidden layer and the rectified linear activation function, and an output layer that must be customized based on the selection of the loss function.
+
Model mengharapkan dua variabel input, memiliki 50 node di hidden layer dan fungsi rectified linear activation, dan lapisan output yang harus di optimasi berdasarkan pemilihan fungsi loss.
  
 
  # define model
 
  # define model
Line 646: Line 641:
 
  model.add(Dense(..., activation='...'))
 
  model.add(Dense(..., activation='...'))
  
−
The model is fit using stochastic gradient descent with a sensible default learning rate of 0.01 and a momentum of 0.9.
+
Model ini cocok menggunakan stochastic gradient descent dengan tingkat pembelajaran default yang masuk akal 0,01 dan momentum 0,9.
  
 
  # compile model
 
  # compile model
Line 652: Line 647:
 
  model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
  
−
The model will be fit for 100 epochs on the training dataset and the test dataset will be used as a validation dataset, allowing us to evaluate both loss and classification accuracy on the train and test sets at the end of each training epoch and draw learning curves.
+
Model ini akan di-fit untuk 100 epoch pada dataset training dan dataset testing akan digunakan sebagai dataset validasi, memungkinkan kita untuk mengevaluasi baik loss dan akurasi klasifikasi dari dataset train dan test di akhir setiap epoch pelatihan dan menggambar kurva learning .
  
 
  # fit model
 
  # fit model
 
  history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
 
  history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
  
−
Now that we have the basis of a problem and model, we can take a look evaluating three common loss functions that are appropriate for a multi-class classification predictive modeling problem.
+
Sekarang kita memiliki dasar masalah dan model, kita dapat melihat mengevaluasi tiga fungsi loss umum yang sesuai untuk multi-class classification predictive modeling problem.
  
−
Although an MLP is used in these examples, the same loss functions can be used when training CNN and RNN models for multi-class classification.
+
Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk multi-class classification.
  
 
===Multi-Class Cross-Entropy Loss===
 
===Multi-Class Cross-Entropy Loss===
  
−
Cross-entropy is the default loss function to use for multi-class classification problems.
+
Cross-entropy adalah fungsi loss default untuk digunakan untuk masalah klasifikasi multi-kelas.
−
 
 
−
In this case, it is intended for use with multi-class classification where the target values are in the set {0, 1, 3, …, n}, where each class is assigned a unique integer value.
 
  
−
Mathematically, it is the preferred loss function under the inference framework of maximum likelihood. It is the loss function to be evaluated first and only changed if you have a good reason.
+
Dalam hal ini, ini dimaksudkan untuk digunakan dengan klasifikasi multi-kelas di mana nilai target berada di set {0, 1, 3, ..., n}, di mana setiap kelas diberi nilai integer unik.
  
−
Cross-entropy will calculate a score that summarizes the average difference between the actual and predicted probability distributions for all classes in the problem. The score is minimized and a perfect cross-entropy value is 0.
+
Secara matematis, ini adalah fungsi loss yang lebih disukai di bawah inference framework of maximum likelihood. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang kuat.
  
−
Cross-entropy can be specified as the loss function in Keras by specifying ‘categorical_crossentropy‘ when compiling the model.
+
Cross-entropy akan menghitung skor yang merangkum perbedaan rata-rata antara distribusi probabilitas aktual dan prediksi untuk semua kelas dalam masalah yang diamati. Skor diminimalkan dan nilai cross-entropy yang sempurna adalah 0.
  
 +
Cross-entropy dapat dispesifikasikan sebagai fungsi loss di Keras dengan menentukan 'categorical_crossentropy ‘saat menyusun model.
  
−
The function requires that the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.
+
Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan n node (satu untuk setiap kelas), dalam hal ini tiga node, dan aktivasi ‘softmax‘ untuk memprediksi probabilitas untuk setiap kelas.
  
 
  model.add(Dense(3, activation='softmax'))
 
  model.add(Dense(3, activation='softmax'))
  
−
In turn, this means that the target variable must be one hot encoded.
+
Pada akhirnya, ini berarti bahwa variabel target harus berupa one hot encoded.
  
−
This is to ensure that each example has an expected probability of 1.0 for the actual class value and an expected probability of 0.0 for all other class values. This can be achieved using the to_categorical() Keras function.
+
Ini untuk memastikan bahwa setiap contoh memiliki probabilitas yang diharapkan dari 1,0 untuk nilai kelas aktual dan probabilitas yang diharapkan dari 0,0 untuk semua nilai kelas lainnya. Ini dapat dicapai dengan menggunakan fungsi to_categorical() Keras.
  
 
  # one hot encode output variable
 
  # one hot encode output variable
 
  y = to_categorical(y)
 
  y = to_categorical(y)
  
−
 
+
Contoh lengkap dari MLP dengan cross-entropy loss untuk masalah klasifikasi multi-kelas tercantum di bawah ini.
−
The complete example of an MLP with cross-entropy loss for the multi-class blobs classification problem is listed below.
 
  
 
  # mlp for the blobs multi-class classification problem with cross-entropy loss
 
  # mlp for the blobs multi-class classification problem with cross-entropy loss
Line 729: Line 722:
 
  pyplot.legend()
 
  pyplot.legend()
  
−
Running the example first prints the classification accuracy for the model on the train and test dataset.
+
Menjalankan contoh pertama-tama mem-print keakuratan klasifikasi untuk model pada dataset train dan test.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see the model performed well, achieving a classification accuracy of about 84% on the training dataset and about 82% on the test dataset.
+
Dalam hal ini, kita dapat melihat model bekerja dengan baik, mencapai akurasi klasifikasi sekitar 84% pada dataset training dan sekitar 82% pada dataset testing.
  
 
  Train: 0.840, Test: 0.822
 
  Train: 0.840, Test: 0.822
  
−
A figure is also created showing two line plots, the top with the cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
+
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan cross-entropy loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan akurasi classification accuracy over epochs..
  
−
In this case, the plot shows the model seems to have converged. The line plots for both cross-entropy and accuracy both show good convergence behavior, although somewhat bumpy. The model may be well configured given no sign of over or under fitting. The learning rate or batch size may be tuned to even out the smoothness of the convergence in this case.
+
Dalam kasus ini, plot menunjukkan model yang tampaknya telah terkonvergensi. Plot garis untuk cross-entropy dan akurasi keduanya menunjukkan perilaku konvergensi yang baik, meskipun agak bergelombang. Model dapat dikonfigurasikan dengan baik tanpa ada tanda-tanda over atau under fitting. Tingkat pembelajaran atau ukuran batch dapat disesuaikan untuk meratakan kelancaran konvergensi dalam kasus ini.
−
Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
 
  
−
Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
+
[[File:Line-Plots-of-Cross-Entropy-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Blobs-Multi-Class-Classification-Problem.png|center|400px|thumb]]
  
 
===Sparse Multiclass Cross-Entropy Loss===
 
===Sparse Multiclass Cross-Entropy Loss===
  
−
A possible cause of frustration when using cross-entropy with classification problems with a large number of labels is the one hot encoding process.
+
Kemungkinan penyebab frustrasi ketika menggunakan cross-entropy dengan masalah klasifikasi dengan sejumlah besar label adalah one hot encoding process.
  
−
For example, predicting words in a vocabulary may have tens or hundreds of thousands of categories, one for each label. This can mean that the target element of each training example may require a one hot encoded vector with tens or hundreds of thousands of zero values, requiring significant memory.
+
Misalnya, memprediksi kata dalam vocabulary dapat memiliki puluhan atau ratusan ribu kategori, satu untuk setiap label. Ini dapat berarti bahwa elemen target dari setiap contoh pelatihan mungkin memerlukan one hot encoded vector yang dikodekan dengan puluhan atau ratusan ribu nilai nol, yang membutuhkan memori yang besar.
  
−
Sparse cross-entropy addresses this by performing the same cross-entropy calculation of error, without requiring that the target variable be one hot encoded prior to training.
+
Sparse cross-entropy dilakukan dengan melakukan perhitungan kesalahan cross-entropy yang sama, tanpa mengharuskan variabel target menjadi one hot encoded sebelum training.
  
−
Sparse cross-entropy can be used in keras for multi-class classification by using ‘sparse_categorical_crossentropy‘ when calling the compile() function.
+
Sparse cross-entropy dapat digunakan dalam keras untuk multi-class classification dengan menggunakan ‘sparse_categorical_crossentropy‘ saat memanggil fungsi compile().
  
 
  model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
  
−
The function requires that the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.
+
Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan n node (satu untuk setiap kelas), dalam hal ini tiga node, dan aktivasi ‘softmax‘ untuk memprediksi probabilitas untuk setiap kelas.
  
 
  model.add(Dense(3, activation='softmax'))
 
  model.add(Dense(3, activation='softmax'))
  
−
No one hot encoding of the target variable is required, a benefit of this loss function.
+
Tidak diperlukan one hot encoding dari variabel target, manfaat dari fungsi loss ini.
  
−
The complete example of training an MLP with sparse cross-entropy on the blobs multi-class classification problem is listed below.
+
Contoh lengkap pelatihan MLP dengan sparse cross-entropy pada blobs multi-class classification problem tercantum di bawah ini.
  
 
  # mlp for the blobs multi-class classification problem with sparse cross-entropy loss
 
  # mlp for the blobs multi-class classification problem with sparse cross-entropy loss
Line 803: Line 795:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the classification accuracy for the model on the train and test dataset.
+
Menjalankan contoh pertama-tama mem-print keakuratan klasifikasi untuk model pada dataset training dan testing.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we can see the model achieves good performance on the problem. In fact, if you repeat the experiment many times, the average performance of sparse and non-sparse cross-entropy should be comparable.
+
Dalam hal ini, kita dapat melihat model mencapai kinerja yang baik pada masalah tersebut. Bahkan, jika anda mengulangi percobaan berkali-kali, kinerja rata-rata sparse dan non-sparse cross-entropy sebanding harus sebanding.
  
 
  Train: 0.832, Test: 0.818
 
  Train: 0.832, Test: 0.818
  
−
A figure is also created showing two line plots, the top with the sparse cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
+
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan sparse cross-entropy loss over epochs untuk dataset train (biru) dan testing (oranye), dan plot bawah menunjukkan classification accuracy over epochs.
 +
 
 +
Dalam hal ini, plot menunjukkan konvergensi yang baik dari model atas pelatihan sehubungan dengan loss dan akurasi klasifikasi.
  
−
In this case, the plot shows good convergence of the model over training with regard to loss and classification accuracy.
 
−
Line Plots of Sparse Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
 
  
−
Line Plots of Sparse Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
+
[[File:Line-Plots-of-Sparse-Cross-Entropy-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Blobs-Multi-Class-Classification-Problem.png|center|400px|thumb]]
  
 
===Kullback Leibler Divergence Loss===
 
===Kullback Leibler Divergence Loss===
  
−
Kullback Leibler Divergence, or KL Divergence for short, is a measure of how one probability distribution differs from a baseline distribution.
+
Singkatnya Kullback Leibler Divergence, atau KL Divergence, adalah ukuran bagaimana satu distribusi probabilitas berbeda dari distribusi baseline.
  
−
A KL divergence loss of 0 suggests the distributions are identical. In practice, the behavior of KL Divergence is very similar to cross-entropy. It calculates how much information is lost (in terms of bits) if the predicted probability distribution is used to approximate the desired target probability distribution.
+
KL divergence loss dengan nilai 0 menunjukkan distribusi identik. Dalam praktiknya, perilaku KL Divergence sangat mirip dengan cross-entropy. Ini menghitung berapa banyak informasi yang hilang (dalam bentuk bit) jika distribusi probabilitas yang diprediksi digunakan untuk memperkirakan distribusi probabilitas target yang diinginkan.
  
−
As such, the KL divergence loss function is more commonly used when using models that learn to approximate a more complex function than simply multi-class classification, such as in the case of an autoencoder used for learning a dense feature representation under a model that must reconstruct the original input. In this case, KL divergence loss would be preferred. Nevertheless, it can be used for multi-class classification, in which case it is functionally equivalent to multi-class cross-entropy.
+
Dengan demikian, fungsi  KL divergence loss lebih umum digunakan ketika menggunakan model yang belajar untuk memperkirakan fungsi yang lebih kompleks daripada hanya klasifikasi multi-kelas, seperti dalam kasus autoencoder yang digunakan untuk mempelajari representasi fitur padat di bawah model yang harus merekonstruksi input asli. Dalam hal ini, KL divergence loss akan lebih disukai. Namun demikian, ini dapat digunakan untuk klasifikasi multi-kelas, dalam hal ini secara fungsional setara dengan multi-class cross-entropy.
  
−
KL divergence loss can be used in Keras by specifying ‘kullback_leibler_divergence‘ in the compile() function.
+
KL divergence loss dapat digunakan dalam Keras dengan men-set ‘kullback_leibler_divergence‘ dalam fungsi compile().
  
 
  model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])
 
  model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])
  
−
As with cross-entropy, the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.
+
Seperti cross-entropy, lapisan output dikonfigurasikan dengan n node (satu untuk setiap kelas), dalam hal ini tiga node, dan aktivasi ‘softmax‘ untuk memprediksi probabilitas untuk setiap kelas.
  
−
Also, as with categorical cross-entropy, we must one hot encode the target variable to have an expected probability of 1.0 for the class value and 0.0 for all other class values.
+
Sama, seperti dengan categorical cross-entropy, kita harus one hot encode variabel target untuk memiliki probabilitas yang diharapkan dari 1,0 untuk nilai kelas dan 0,0 untuk semua nilai kelas lainnya.
  
 
  # one hot encode output variable
 
  # one hot encode output variable
 
  y = to_categorical(y)
 
  y = to_categorical(y)
  
−
The complete example of training an MLP with KL divergence loss for the blobs multi-class classification problem is listed below.
+
Contoh lengkap pelatihan MLP dengan KL divergence loss untuk blobs multi-class classification problem tercantum di bawah ini.
  
 
  # mlp for the blobs multi-class classification problem with kl divergence loss
 
  # mlp for the blobs multi-class classification problem with kl divergence loss
Line 881: Line 873:
 
  pyplot.show()
 
  pyplot.show()
  
−
Running the example first prints the classification accuracy for the model on the train and test dataset.
+
Menjalankan contoh pertama-tama mem-print keakuratan klasifikasi untuk model pada dataset training dan testing.
  
−
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
+
Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.
  
−
In this case, we see performance that is similar to those results seen with cross-entropy loss, in this case about 82% accuracy on the train and test dataset.
+
Dalam hal ini, kita melihat kinerja yang mirip dengan hasil yang terlihat dengan cross-entropy loss, dalam hal ini akurasi sekitar 82% pada dataset training dan testing.
  
 
  Train: 0.822, Test: 0.822
 
  Train: 0.822, Test: 0.822
  
−
A figure is also created showing two line plots, the top with the KL divergence loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
+
Gambar juga dibuat menunjukkan dua plot garis, bagian atas KL divergence loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan classification accuracy over epochs.
−
 
 
−
In this case, the plot shows good convergence behavior for both loss and classification accuracy. It is very likely that an evaluation of cross-entropy would result in nearly identical behavior given the similarities in the measure.
 
−
Line Plots of KL Divergence Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
 
−
 
 
−
Line Plots of KL Divergence Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem
 
−
 
 
−
==Further Reading==
 
−
 
 
−
This section provides more resources on the topic if you are looking to go deeper.
 
−
 
 
−
Posts
 
−
 
 
−
* Loss and Loss Functions for Training Deep Learning Neural Networks
 
−
 
 
−
Papers
 
−
* On Loss Functions for Deep Neural Networks in Classification, 2017.
 
−
 
 
−
 
 
  
 +
Dalam kasus ini, plot menunjukkan perilaku konvergensi yang baik untuk loss dan akurasi klasifikasi. Sangat mungkin bahwa evaluasi cross-entropy akan menghasilkan perilaku yang hampir identik mengingat kesamaan dalam ukuran.
  
  
 +
[[File:Line-Plots-of-KL-Divergence-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Blobs-Multi-Class-Classification-Problem.png|center|400px|thumb]]
  
 
==Referensi==
 
==Referensi==
  
 
* https://machinelearningmastery.com/how-to-choose-loss-functions-when-training-deep-learning-neural-networks/
 
* https://machinelearningmastery.com/how-to-choose-loss-functions-when-training-deep-learning-neural-networks/
−
 
  
 
==Pranala Menarik==
 
==Pranala Menarik==
  
 
* [[Keras]]
 
* [[Keras]]
 +
* [[Keras: Loss and Loss Function]]
 
* [[Python]]
 
* [[Python]]

Latest revision as of 10:16, 30 August 2019

Sumber: https://machinelearningmastery.com/how-to-choose-loss-functions-when-training-deep-learning-neural-networks/


Deep learning neural network di-train dengan menggunakan algoritma stochastic gradient descent optimization.

Sebagai bagian dari optimisasi algoritma, kesalahan kondisi model harus diperkirakan berulang kali. Ini membutuhkan pilihan fungsi kesalahan, secara konvensional disebut fungsi loss, yang dapat digunakan untuk memperkirakan loss model sehingga weight dapat diperbarui untuk mengurangi loss pada evaluasi selanjutnya.

Neural network model mempelajari pemetaan dari input ke output dari contoh dan pilihan fungsi loss harus sesuai dengan framing masalah pemodelan prediktif spesifik, seperti klasifikasi atau regresi. Lebih lanjut, konfigurasi lapisan keluaran juga harus sesuai untuk fungsi loss yang dipilih.

Dalam tutorial ini, kita akan mempelajari cara memilih fungsi loss untuk deep learning neural network untuk masalah pemodelan prediktif yang diberikan.

Sesudah menyelesaikan tutorial ini, anda akan mengetahui:

  • Bagaimana mengkonfigurasi model untuk mean squared error dan varian-nya untuk regression problems.
  • Bagaimana mengkonfigurasi model untuk cross-entropy dan fungsi hinge loss untuk binary classification.
  • Bagaimana mengkonfigurasi model untuk cross-entropy dan fungsi KL divergence loss untuk multi-class classification.

Tutorial Overview

Tutorial ini di bagi dalam tiga bagian, yaitu: 

Regression Loss Functions
    Mean Squared Error Loss
    Mean Squared Logarithmic Error Loss
    Mean Absolute Error Loss
Binary Classification Loss Functions
    Binary Cross-Entropy
    Hinge Loss
    Squared Hinge Loss
Multi-Class Classification Loss Functions
    Multi-Class Cross-Entropy Loss
    Sparse Multiclass Cross-Entropy Loss
    Kullback Leibler Divergence Loss

Kita akan fokus pada bagaimana memilih dan mengimplementasikan berbagai fungsi loss. Untuk teori lebih lanjut tentang fungsi loss, bisa lihat tulisan:

Regression Loss Function

Masalah pemodelan prediktif regresi melibatkan memprediksi kuantitas yang bernilai nyata. Pada bagian ini, kita akan menyelidiki fungsi loss yang sesuai untuk masalah pemodelan prediksi regresi.

Sebagai konteks untuk investigasi ini, kami akan menggunakan generator masalah regresi standar yang disediakan oleh perpustakaan scikit-learn di fungsi make_regress(). Fungsi ini akan menghasilkan contoh-contoh dari masalah regresi sederhana dengan sejumlah variabel input, noise statistik, dan properti lainnya.

Kita akan menggunakan fungsi ini untuk mendefinisikan masalah yang memiliki 20 fitur input; 10 fitur bermakna dan 10 tidak relevan. Sebanyak 1.000 contoh akan dihasilkan secara acak. Generator angka pseudorandom akan diperbaiki untuk memastikan bahwa kami mendapatkan 1.000 contoh yang sama setiap kali kode dijalankan. 

# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)

Neural network umumnya berkinerja lebih baik ketika variabel input dan output bernilai real yang di skalakan (scaled) pada kisaran yang masuk akal. Untuk masalah ini, masing-masing variabel input dan variabel target memiliki distribusi Gaussian; oleh karena itu, standarisasi data dalam hal ini dibutuhkan.

Kita dapat mencapai ini menggunakan kelas transformator StandardScaler juga dari library scikit-learn. Pada masalah yang sebenarnya, kita akan menyiapkan scaler pada set data training dan menerapkannya pada set train dan test, tetapi untuk menyederhanakan, kita akan menskalakan semua data bersama sebelum dipecah menjadi set train dan test. 

# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]

Setelah di skalakan, data dibagi rata menjadi set train dan test. 

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]

Model Multilayer Perceptron (MLP) yang kecil akan didefinisikan untuk mengatasi masalah ini dan memberikan dasar untuk mengeksplorasi berbagai fungsi kerugian.

Model akan mengharapkan 20 fitur sebagai input sebagaimana didefinisikan oleh masalah. Model akan memiliki satu lapisan tersembunyi dengan 25 node dan akan menggunakan fungsi rectified linear activation (ReLU). Lapisan output akan memiliki 1 simpul, mengingat satu nilai riil yang akan diprediksi, dan akan menggunakan fungsi aktivasi linier. 

# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))

Model ini akan cocok dengan stochastic gradient descent dengan learning rate 0,01 dan momentum 0,9, keduanya nilai default yang cukup baik.

Training akan dilakukan sebanyak 100 epoch dan set test akan dievaluasi pada akhir setiap epoch sehingga kita dapat merencanakan kurva learning di akhir run. 

opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)

Sekarang kita memiliki dasar masalah dan model, kita dapat mengevaluasi tiga fungsi loss umum yang sesuai untuk masalah pemodelan prediksi regresi.

Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk regresi.

Mean Squared Error Loss

Mean Squared Error, atau MSE, loss adalah default loss yang digunakan untuk masalah regresi.

Secara matematis, ini adalah fungsi loss yang disukai di bawah inference framework of maximum likelihood jika distribusi variabel target adalah Gaussian. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang bagus.

Mean squared error dihitung sebagai rata-rata perbedaan kuadrat antara nilai yang diprediksi dan yang sebenarnya. Hasilnya selalu positif terlepas dari tanda nilai yang diprediksi dan aktual dan nilai sempurna adalah 0,0. Kuadrat berarti bahwa kesalahan yang lebih besar menghasilkan lebih banyak kesalahan daripada kesalahan yang lebih kecil, yang berarti bahwa model akan dihukum karena membuat kesalahan yang lebih besar.

Fungsi mean squared error loss dapat digunakan dalam Keras dengan menuliskan ‘mse‘ atau ‘mean_squared_error‘ sebagai fungsi loss saat menyusun model. 

model.compile(loss='mean_squared_error')

Disarankan bahwa layer output memiliki satu simpul untuk variabel target dan fungsi aktivasi linier digunakan. 

model.add(Dense(1, activation='linear'))

Contoh lengkap menunjukkan MLP pada masalah regresi yang dijelaskan tercantum di bawah ini. 

# mlp for regression with mse loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_error', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

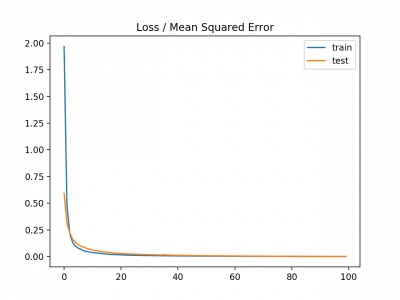
Menjalankan contoh pertama mem-print kesalahan kuadrat rata-rata model pada train dan test dataset.

Mengingat sifat stokastik dari algoritma training, Basil spesifik dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam kasus ini, kita dapat melihat bahwa model berusaha mencapai nol kesalahan, setidaknya sampai tiga tempat desimal. 

Train: 0.000, Test: 0.001

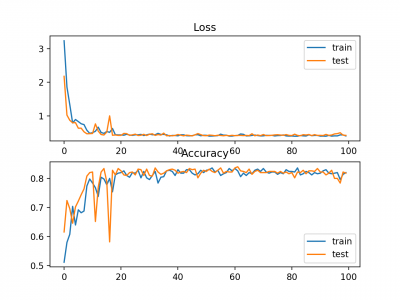
Plot garis juga dibuat menunjukkan mean squared error loss selama periode pelatihan untuk set train (biru) dan test (oranye).

Kita dapat melihat bahwa model terkonvergensi dengan cukup cepat dan baik kinerja train dan test tetap setara. Perilaku kinerja dan konvergensi model menunjukkan bahwa mean squared error cocok untuk neural network yang mempelajari masalah ini.

Line-plot-of-Mean-Squared-Error-Loss-over-Training-Epochs-When-Optimizing-the-Mean-Squared-Error-Loss-Function.png

Mean Squared Logarithmic Error Loss

Mungkin ada masalah regresi di mana nilai target memiliki penyebaran nilai dan ketika memprediksi nilai besar, kita mungkin tidak ingin menghukum model sebanyak kesalahan kuadrat rata-rata.

Sebagai gantinya, kita pertama-tama dapat menghitung nilai log dari masing-masing nilai yang diprediksi, lalu menghitung rata-rata kesalahan kuadrat. Ini disebut Mean Squared Logarithmic Error loss, atau disingkat MSLE.

Ini memiliki efek membuat santai efek punishing saat ada perbedaan besar dalam nilai prediksi yang besar.

Sebagai ukuran loss, mungkin lebih tepat ketika model memprediksi unscaled quantities secara langsung. Namun demikian, kita dapat menunjukkan fungsi loss ini menggunakan masalah regresi sederhana.

Model ini dapat diperbarui untuk menggunakan fungsi loss ‘mean_squared_logarithmic_error‘ dan mempertahankan konfigurasi yang sama untuk layer output. Kita juga akan melacak mean squared error sebagai metrik saat memasang model sehingga kita dapat menggunakannya sebagai ukuran kinerja dan plot kurva pembelajaran. 

model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])

Contoh lengkap menggunakan fungsi loss MSLE tercantum di bawah ini. 

# mlp for regression with msle loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh pertama mem-print mean squared error untuk model pada datset train dan test.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh tersebut beberapa kali.

Dalam hal ini, kita dapat melihat bahwa model tersebut menghasilkan MSE yang sedikit lebih buruk pada datset training dan testing. Ini mungkin tidak cocok untuk masalah ini karena distribusi variabel target adalah standar Gaussian. 

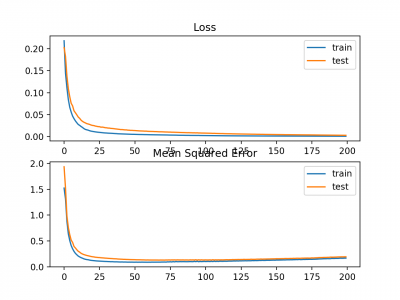
Train: 0.165, Test: 0.184

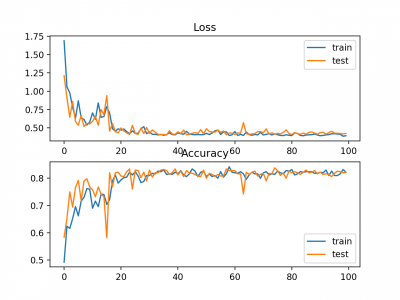
Plot garis juga dibuat menunjukkan mean squared logarithmic error losst selama periode training untuk set train (biru) dan test (oranye) (atas), dan plot yang sama untuk mean squared error (bawah).

Kita dapat melihat bahwa algoritma MSLE konvergen lebih dari a100 epoch; tampaknya MSE mungkin menunjukkan tanda-tanda overfitting dari masalah yang ada, jatuh secara cepat cepat dan mulai naik pada epoch 20 dan seterusnya.


Line-plots-of-Mean-Squared-Logistic-Error-Loss-and-Mean-Squared-Error-over-Training-Epochs.png

Mean Absolute Error Loss

Pada beberapa masalah regresi, distribusi variabel target mungkin sebagian besar Gaussian, tetapi mungkin memiliki outlier, mis. nilai besar atau kecil jauh dari nilai rata-rata.

The Mean Absolute Error loss, atau MAE, adalah fungsi loss yang sesuai dalam kasus ini karena itu lebih kuat untuk outlier. Ini dihitung sebagai rata-rata perbedaan absolut antara nilai aktual dan prediksi.

Model dapat diperbarui untuk menggunakan fungsi loss ‘mean_absolute_error‘ dan mempertahankan konfigurasi yang sama untuk layer output. 

model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])

Contoh lengkap menggunakan mean absolute error sebagai fungsi loss pada masalah test regresi terlampir di bawah ini. 

# mlp for regression with mae loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh pertama mem-print mean squared error untuk model dataset train dan test.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam kasus ini, kita dapat melihat bahwa model learn masalah, mencapai kesalahan mendekati nol, setidaknya ke tiga tempat desimal. 

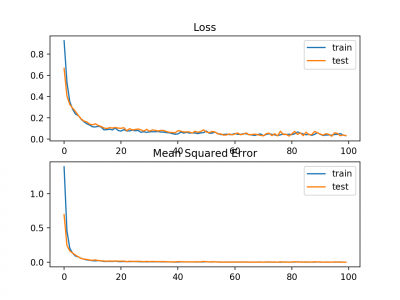
Train: 0.002, Test: 0.002

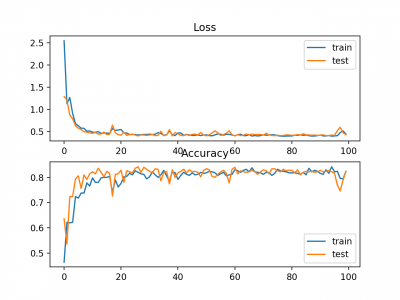
Plot garis juga dibuat yang menunjukkan mean absolute error loss selama periode pelatihan untuk set train (biru) dan test (oranye) (atas), dan plot serupa untuk mean squared error (bawah).

Dalam hal ini, kita dapat melihat bahwa MAE memang konvergen akan tetapi pencapaiannya bergelombang, meskipun dinamika MSE tidak tampak sangat terpengaruh. Kita tahu bahwa variabel target adalah Gaussian standar tanpa outlier besar, sehingga MAE tidak cocok untuk kasus ini.

Mungkin lebih tepat untuk masalah ini jika kita tidak menskalakan variabel target terlebih dahulu.

Line-plots-of-Mean-Absolute-Error-Loss-and-Mean-Squared-Error-over-Training-Epochs.png

Binary Classification Loss Function

Klasifikasi biner adalah masalah-masalah pemodelan prediktif di mana contoh diberikan satu dari dua label.

Masalahnya sering di lihat sebagai memprediksi nilai 0 atau 1 untuk kelas pertama atau kedua dan sering diimplementasikan sebagai memprediksi probabilitas milik nilai kelas 1.

Pada bagian ini, kami akan menyelidiki fungsi kerugian yang sesuai untuk masalah pemodelan prediktif klasifikasi biner.

Kami akan menghasilkan contoh dari masalah test lingkaran di scikit-belajar sebagai basis untuk penelitian ini. Masalah lingkaran melibatkan sampel yang diambil dari dua lingkaran konsentris pada bidang dua dimensi, di mana titik pada lingkaran luar milik kelas 0 dan titik untuk lingkaran dalam milik kelas 1. Noise statistik ditambahkan ke sampel untuk menambah ambiguitas dan membuat masalahnya lebih sulit untuk dipelajari.

Kami akan men-generate 1.000 contoh dan menambahkan 10% noise statistik. Generator nomor pseudorandom akan di-seed dengan nilai yang sama untuk memastikan bahwa kami selalu mendapatkan 1.000 contoh yang sama. 

# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)

Kita dapat membuat scatter plot dataset untuk mendapatkan gambaran tentang masalah yang kita modelkan. Contoh lengkapnya tercantum di bawah ini. 

# scatter plot of the circles dataset with points colored by class
from sklearn.datasets import make_circles
from numpy import where
from matplotlib import pyplot
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# select indices of points with each class label
for i in range(2):
	samples_ix = where(y == i)
	pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i))
pyplot.legend()
pyplot.show()

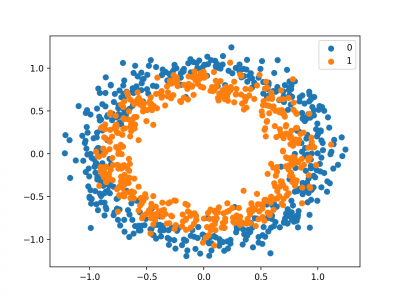
Menjalankan contoh menciptakan scatter plot contoh, di mana variabel input menentukan lokasi titik dan nilai kelas mendefinisikan warna, dengan kelas 0 biru dan oranye kelas 1.

Scatter-Plot-of-Dataset-for-the-Circles-Binary-Classification-Problem.png

Poin sudah diskalakan dengan cukup sekitar 0, hampir di [-1,1]. Kita tidak akan mengubah skala mereka dalam hal ini.

Dataset akan di split sama untuk train dan test set. 

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

Model MLP sederhana dapat didefinisikan untuk mengatasi masalah ini yang mengharapkan dua input untuk dua fitur dalam dataset, lapisan tersembunyi dengan 50 node, fungsi aktivasi linear yang diperbaiki dan lapisan output yang perlu dikonfigurasi untuk pilihan fungsi loss. 

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='...'))

Model ini akan cocok menggunakan stochastic gradient descent dengan tingkat pembelajaran default yang masuk akal 0,01 dan momentum 0,9. 

opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])

Kami akan mencocokkan model untuk 200 training epoch dan mengevaluasi kinerja model terhadap loss dan akurasi pada akhir setiap epoch sehingga kami dapat mem-plot kurva pembelajaran. 

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

Sekarang kita memiliki dasar masalah dan model, kita dapat melihat mengevaluasi tiga fungsi loss umum yang sesuai untuk masalah pemodelan prediktif klasifikasi biner.

Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk klasifikasi biner.

Binary Cross-Entropy Loss

Cross-entropy adalah fungsi loss default yang digunakan untuk masalah klasifikasi biner.

Ini dimaksudkan untuk digunakan dengan klasifikasi biner di mana nilai target berada di set {0, 1}.

Secara matematis, ini adalah fungsi loss yang lebih disukai di bawah inference framework of maximum likelihood. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang bagus.

Cross-entropy akan menghitung skor yang merangkum perbedaan rata-rata antara distribusi probabilitas aktual dan prediksi untuk kelas prediksi 1. Skor tersebut diminimalkan dan nilai cross-entropy yang baik adalah 0.

Cross-entropy dapat ditentukan sebagai fungsi loss di Keras dengan menetapkan ‘binary_crossentropy‘ saat menyusun model. 

model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])

Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan satu simpul dan aktivasi ‘sigmoid in untuk memprediksi probabilitas untuk kelas 1. 

model.add(Dense(1, activation='sigmoid'))

Contoh lengkap dari MLP dengan kehilangan lintas-entropi untuk masalah klasifikasi biner dua lingkaran tercantum di bawah ini. 

# mlp for the circles problem with cross entropy loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh untuk mem-print akurasi klasifikasi untuk model pada dataset train dan test.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam hal ini, kita dapat melihat bahwa model bisa learn masalah dengan cukup baik, mencapai akurasi sekitar 83% pada dataset train dan sekitar 85% pada dataset test. Skor cukup dekat, menunjukkan bahwa model yang di peroleh mungkin tidak over atau underfit. 

Train: 0.836, Test: 0.852

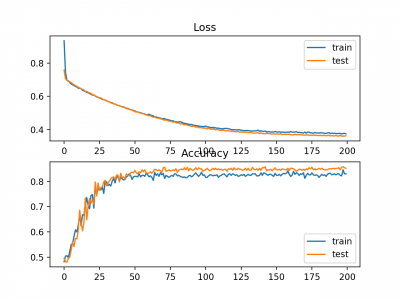
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan cross-entropy loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan classification accuracy over epochs.

Plot menunjukkan bahwa proses trainig konvergsi dengan baik. Plot untuk loss baik, mengingat sifat kesalahan yang kontinyu antara distribusi probabilitas, sedangkan plot garis untuk akurasi menunjukkan adanya tonjolan, memberikan contoh dataset train dan test pada akhirnya hanya dapat diprediksi sebagai benar atau salah, memberikan umpan balik yang kurang terperinci pada kinerja.

Line-Plots-of-Cross-Entropy-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Two-Circles-Binary-Classification-Problem.png

Hinge Loss

Alternatif untuk cross-entropy untuk masalah klasifikasi biner adalah fungsi hinge loss, terutama dikembangkan untuk digunakan dengan model Support Vector Machine (SVM).

Ini dimaksudkan untuk digunakan dengan klasifikasi biner di mana nilai target berada di set {-1, 1}.

Fungsi kehilangan engsel mendorong contoh untuk memiliki tanda yang benar, menetapkan lebih banyak kesalahan ketika ada perbedaan dalam tanda antara nilai kelas aktual dan prediksi.

Laporan kinerja dengan hinge loss beragam, kadang-kadang menghasilkan kinerja yang lebih baik daripada cross-entropy pada masalah klasifikasi biner.

Pertama, variabel target harus dimodifikasi untuk memiliki nilai dalam set {-1, 1}. 

# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1

Fungsi hinge loss dapat diset ‘hinge‘ dalam fungsi compile. 

model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])

Akhirnya, lapisan output dari jaringan harus dikonfigurasi untuk memiliki satu simpul dengan fungsi aktivasi hyperbolic tangent yang mampu menghasilkan nilai tunggal dalam kisaran [-1, 1]. 

model.add(Dense(1, activation='tanh'))

Contoh lengkap MLP dengan fungsi hinge loss untuk two circles binary classification problem tercantum di bawah ini. 

# mlp for the circles problem with hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh pertama-tama mem-print classification accuracy untuk model pada dataset train dan test.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam hal ini, kita dapat melihat kinerja yang sedikit lebih buruk daripada menggunakan cross-entropy, dengan konfigurasi model yang dipilih dengan akurasi kurang dari 80% pada dataset train dan test. 

Train: 0.792, Test: 0.740

A figure is also created showing two line plots, the top with the hinge loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.

Plot hinge loss menunjukkan bahwa model telah konvergen dan memiliki loss yang wajar pada kedua dataset. Alur akurasi klasifikasi juga menunjukkan tanda-tanda konvergensi, meskipun pada tingkat kinerja yang lebih rendah daripada yang diinginkan pada masalah ini.


Line-Plots-of-Hinge-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Two-Circles-Binary-Classification-Problem.png

Squared Hinge Loss

Fungsi hinge loss memiliki banyak pengembangan, seringkali menjadi subjek investigasi dengan model SVM.

Pengembangan yang populer disebut squared hinge loss yang hanya menghitung kuadrat dari score hinge loss. Ini memiliki efek menghaluskan permukaan fungsi kesalahan dan membuatnya lebih mudah untuk dikerjakan secara numerik.

Jika menggunakan hinge loss memang menghasilkan kinerja yang lebih baik pada masalah klasifikasi biner yang diberikan, kemungkinan bahwa squared hinge loss mungkin sesuai.

Seperti halnya menggunakan fungsi hinge loss, variabel target harus dimodifikasi untuk memiliki nilai dalam set {-1, 1}. 

# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1

Squared hinge loss dapat ditentukan sebagai ‘squared_hinge‘ dalam fungsi compile() saat mendefinisikan model. 

model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])

Dan akhirnya, lapisan output harus menggunakan node tunggal dengan fungsi aktivasi tangen hiperbolik yang mampu menghasilkan nilai kontinu dalam kisaran [-1, 1]. 

model.add(Dense(1, activation='tanh'))

Contoh lengkap dari MLP dengan fungsi squared hinge loss pada masalah klasifikasi biner dua lingkaran tercantum di bawah ini. 

# mlp for the circles problem with squared hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh pertama-tama memprint keakuratan klasifikasi untuk model pada dataset train dan test.

Mengingat sifat stokastik dari algoritma pelatihan, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam kasus ini, kita dapat melihat bahwa untuk masalah ini dan konfigurasi model yang dipilih, hinge squared loss mungkin tidak sesuai, sehingga akurasi klasifikasi kurang dari 70% pada dataset train dan test. 

Train: 0.682, Test: 0.646

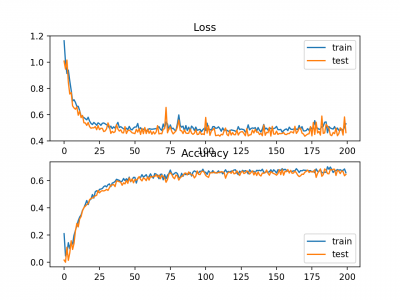
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan squared hinge loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan classification accuracy over epochs.

Plot loss menunjukkan bahwa memang, model konvergensi, tetapi bentuk permukaan error tidak semulus fungsi loss lainnya di mana perubahan kecil pada nilai weight menyebabkan perubahan besar loss.

Line-Plots-of-Squared-Hinge-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Two-Circles-Binary-Classification-Problem.png

Multi-Class Classification Loss Functions

Multi-Class classification adalah masalah-masalah pemodelan prediktif di mana contoh diberikan satu dari lebih dari dua kelas.

Masalahnya sering di frame untuk memprediksi nilai integer, di mana setiap kelas diberi nilai integer unik dari 0 hingga (num_classes - 1). Masalahnya sering diimplementasikan sebagai memprediksi probabilitas dari contoh milik masing-masing kelas yang dikenal.

Pada bagian ini, kita akan melihat fungsi loss yang sesuai untuk multi-class classification predictive modeling problems.

Kita akan menggunakan masalah blobs sebagai dasar untuk penelitian. Fungsi make_blobs() yang disediakan oleh scikit-learn menyediakan cara untuk men-generate contoh yang diberikan sejumlah kelas dan fitur input tertentu. Kita akan menggunakan fungsi ini untuk menghasilkan 1.000 contoh untuk masalah klasifikasi 3-kelas dengan 2 variabel input. Generator nomor pseudorandom akan di-seed secara konsisten sehingga 1.000 contoh yang sama dihasilkan setiap kali kode dijalankan. 

# generate dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)

Dua variabel input dapat diambil sebagai koordinat x dan y untuk titik pada bidang dua dimensi.

Contoh di bawah ini membuat sebaran plot dari seluruh titik pewarnaan dataset oleh keanggotaan kelas mereka. 

# scatter plot of blobs dataset
from sklearn.datasets.samples_generator import make_blobs
from numpy import where
from matplotlib import pyplot
# generate dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# select indices of points with each class label
for i in range(3):
	samples_ix = where(y == i)
	pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1])
pyplot.show()

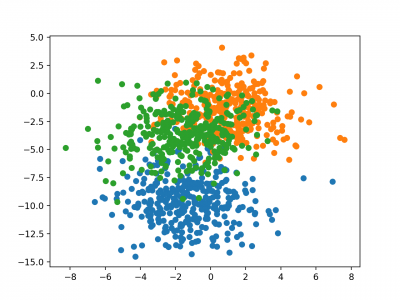
Menjalankan contoh membuat scatter plot yang menunjukkan 1.000 contoh dalam dataset dengan contoh milik kelas 0, 1, dan 2 warna biru, oranye, dan hijau.

Scatter-Plot-of-Examples-Generated-from-the-Blobs-Multi-Class-Classification-Problem.png

Fitur input Gaussian dan dapat mengambil manfaat dari standardisasi; namun demikian, kita akan menjaga nilai-nilai tetap dalam contoh ini untuk mempersingkat.

Dataset akan dibagi secara merata antara dataset training dan testing. 

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

Model MLP kecil akan digunakan sebagai dasar untuk mengeksplorasi fungsi loss.

Model mengharapkan dua variabel input, memiliki 50 node di hidden layer dan fungsi rectified linear activation, dan lapisan output yang harus di optimasi berdasarkan pemilihan fungsi loss. 

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(..., activation='...'))

Model ini cocok menggunakan stochastic gradient descent dengan tingkat pembelajaran default yang masuk akal 0,01 dan momentum 0,9. 

# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])

Model ini akan di-fit untuk 100 epoch pada dataset training dan dataset testing akan digunakan sebagai dataset validasi, memungkinkan kita untuk mengevaluasi baik loss dan akurasi klasifikasi dari dataset train dan test di akhir setiap epoch pelatihan dan menggambar kurva learning . 

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)

Sekarang kita memiliki dasar masalah dan model, kita dapat melihat mengevaluasi tiga fungsi loss umum yang sesuai untuk multi-class classification predictive modeling problem.

Meskipun MLP digunakan dalam contoh-contoh ini, fungsi loss yang sama dapat digunakan ketika melatih model CNN dan RNN untuk multi-class classification.

Multi-Class Cross-Entropy Loss

Cross-entropy adalah fungsi loss default untuk digunakan untuk masalah klasifikasi multi-kelas.

Dalam hal ini, ini dimaksudkan untuk digunakan dengan klasifikasi multi-kelas di mana nilai target berada di set {0, 1, 3, ..., n}, di mana setiap kelas diberi nilai integer unik.

Secara matematis, ini adalah fungsi loss yang lebih disukai di bawah inference framework of maximum likelihood. Ini adalah fungsi loss yang harus dievaluasi terlebih dahulu dan hanya diubah jika anda memiliki alasan yang kuat.

Cross-entropy akan menghitung skor yang merangkum perbedaan rata-rata antara distribusi probabilitas aktual dan prediksi untuk semua kelas dalam masalah yang diamati. Skor diminimalkan dan nilai cross-entropy yang sempurna adalah 0.

Cross-entropy dapat dispesifikasikan sebagai fungsi loss di Keras dengan menentukan 'categorical_crossentropy ‘saat menyusun model.

Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan n node (satu untuk setiap kelas), dalam hal ini tiga node, dan aktivasi ‘softmax‘ untuk memprediksi probabilitas untuk setiap kelas. 

model.add(Dense(3, activation='softmax'))

Pada akhirnya, ini berarti bahwa variabel target harus berupa one hot encoded.

Ini untuk memastikan bahwa setiap contoh memiliki probabilitas yang diharapkan dari 1,0 untuk nilai kelas aktual dan probabilitas yang diharapkan dari 0,0 untuk semua nilai kelas lainnya. Ini dapat dicapai dengan menggunakan fungsi to_categorical() Keras. 

# one hot encode output variable
y = to_categorical(y)

Contoh lengkap dari MLP dengan cross-entropy loss untuk masalah klasifikasi multi-kelas tercantum di bawah ini. 

# mlp for the blobs multi-class classification problem with cross-entropy loss
from sklearn.datasets.samples_generator import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()

Menjalankan contoh pertama-tama mem-print keakuratan klasifikasi untuk model pada dataset train dan test.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam hal ini, kita dapat melihat model bekerja dengan baik, mencapai akurasi klasifikasi sekitar 84% pada dataset training dan sekitar 82% pada dataset testing. 

Train: 0.840, Test: 0.822

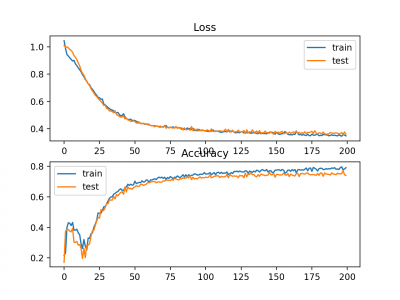
Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan cross-entropy loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan akurasi classification accuracy over epochs..

Dalam kasus ini, plot menunjukkan model yang tampaknya telah terkonvergensi. Plot garis untuk cross-entropy dan akurasi keduanya menunjukkan perilaku konvergensi yang baik, meskipun agak bergelombang. Model dapat dikonfigurasikan dengan baik tanpa ada tanda-tanda over atau under fitting. Tingkat pembelajaran atau ukuran batch dapat disesuaikan untuk meratakan kelancaran konvergensi dalam kasus ini.

Line-Plots-of-Cross-Entropy-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Blobs-Multi-Class-Classification-Problem.png

Sparse Multiclass Cross-Entropy Loss

Kemungkinan penyebab frustrasi ketika menggunakan cross-entropy dengan masalah klasifikasi dengan sejumlah besar label adalah one hot encoding process.

Misalnya, memprediksi kata dalam vocabulary dapat memiliki puluhan atau ratusan ribu kategori, satu untuk setiap label. Ini dapat berarti bahwa elemen target dari setiap contoh pelatihan mungkin memerlukan one hot encoded vector yang dikodekan dengan puluhan atau ratusan ribu nilai nol, yang membutuhkan memori yang besar.

Sparse cross-entropy dilakukan dengan melakukan perhitungan kesalahan cross-entropy yang sama, tanpa mengharuskan variabel target menjadi one hot encoded sebelum training.

Sparse cross-entropy dapat digunakan dalam keras untuk multi-class classification dengan menggunakan ‘sparse_categorical_crossentropy‘ saat memanggil fungsi compile(). 

model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

Fungsi ini mensyaratkan bahwa lapisan output dikonfigurasikan dengan n node (satu untuk setiap kelas), dalam hal ini tiga node, dan aktivasi ‘softmax‘ untuk memprediksi probabilitas untuk setiap kelas. 

model.add(Dense(3, activation='softmax'))

Tidak diperlukan one hot encoding dari variabel target, manfaat dari fungsi loss ini.

Contoh lengkap pelatihan MLP dengan sparse cross-entropy pada blobs multi-class classification problem tercantum di bawah ini. 

# mlp for the blobs multi-class classification problem with sparse cross-entropy loss
from sklearn.datasets.samples_generator import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh pertama-tama mem-print keakuratan klasifikasi untuk model pada dataset training dan testing.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam hal ini, kita dapat melihat model mencapai kinerja yang baik pada masalah tersebut. Bahkan, jika anda mengulangi percobaan berkali-kali, kinerja rata-rata sparse dan non-sparse cross-entropy sebanding harus sebanding. 

Train: 0.832, Test: 0.818

Gambar juga dibuat menunjukkan dua plot garis, bagian atas dengan sparse cross-entropy loss over epochs untuk dataset train (biru) dan testing (oranye), dan plot bawah menunjukkan classification accuracy over epochs.

Dalam hal ini, plot menunjukkan konvergensi yang baik dari model atas pelatihan sehubungan dengan loss dan akurasi klasifikasi.


Line-Plots-of-Sparse-Cross-Entropy-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Blobs-Multi-Class-Classification-Problem.png

Kullback Leibler Divergence Loss

Singkatnya Kullback Leibler Divergence, atau KL Divergence, adalah ukuran bagaimana satu distribusi probabilitas berbeda dari distribusi baseline.

KL divergence loss dengan nilai 0 menunjukkan distribusi identik. Dalam praktiknya, perilaku KL Divergence sangat mirip dengan cross-entropy. Ini menghitung berapa banyak informasi yang hilang (dalam bentuk bit) jika distribusi probabilitas yang diprediksi digunakan untuk memperkirakan distribusi probabilitas target yang diinginkan.

Dengan demikian, fungsi KL divergence loss lebih umum digunakan ketika menggunakan model yang belajar untuk memperkirakan fungsi yang lebih kompleks daripada hanya klasifikasi multi-kelas, seperti dalam kasus autoencoder yang digunakan untuk mempelajari representasi fitur padat di bawah model yang harus merekonstruksi input asli. Dalam hal ini, KL divergence loss akan lebih disukai. Namun demikian, ini dapat digunakan untuk klasifikasi multi-kelas, dalam hal ini secara fungsional setara dengan multi-class cross-entropy.

KL divergence loss dapat digunakan dalam Keras dengan men-set ‘kullback_leibler_divergence‘ dalam fungsi compile(). 

model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])

Seperti cross-entropy, lapisan output dikonfigurasikan dengan n node (satu untuk setiap kelas), dalam hal ini tiga node, dan aktivasi ‘softmax‘ untuk memprediksi probabilitas untuk setiap kelas.

Sama, seperti dengan categorical cross-entropy, kita harus one hot encode variabel target untuk memiliki probabilitas yang diharapkan dari 1,0 untuk nilai kelas dan 0,0 untuk semua nilai kelas lainnya. 

# one hot encode output variable
y = to_categorical(y)

Contoh lengkap pelatihan MLP dengan KL divergence loss untuk blobs multi-class classification problem tercantum di bawah ini. 

# mlp for the blobs multi-class classification problem with kl divergence loss
from sklearn.datasets.samples_generator import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()

Menjalankan contoh pertama-tama mem-print keakuratan klasifikasi untuk model pada dataset training dan testing.

Mengingat sifat stokastik dari algoritma training, hasil spesifik anda dapat bervariasi. Coba jalankan contoh beberapa kali.

Dalam hal ini, kita melihat kinerja yang mirip dengan hasil yang terlihat dengan cross-entropy loss, dalam hal ini akurasi sekitar 82% pada dataset training dan testing. 

Train: 0.822, Test: 0.822

Gambar juga dibuat menunjukkan dua plot garis, bagian atas KL divergence loss over epochs untuk dataset train (biru) dan test (oranye), dan plot bawah menunjukkan classification accuracy over epochs.

Dalam kasus ini, plot menunjukkan perilaku konvergensi yang baik untuk loss dan akurasi klasifikasi. Sangat mungkin bahwa evaluasi cross-entropy akan menghasilkan perilaku yang hampir identik mengingat kesamaan dalam ukuran.


Line-Plots-of-KL-Divergence-Loss-and-Classification-Accuracy-over-Training-Epochs-on-the-Blobs-Multi-Class-Classification-Problem.png

Referensi

Pranala Menarik

Retrieved from "https://onnocenter.or.id/wiki/index.php?title=Keras:_Memilih_Fungsi_Loss&oldid=56979"